题目内容
17. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,M是棱PC上一点,PA∥平面MOB;
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,O为AD的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$,M是棱PC上一点,PA∥平面MOB; (1)证明:CD⊥平面PAD;
(2)求证:M是棱PC的中点;
(3)求三棱锥M-POB的体积.
分析 (1)由CD⊥AD,利用面面垂直的性质定理即可得出CD⊥底面PAD.
(2)连接AC交OB于点N,连接MN.由BC∥AO,BC=AO,可得AN=NC.再利用线面平行的性质定理可得AP∥MN,即可证明.
(3)由PA=PD=2=AD,OA=OD,可得PO⊥AD.利用面面垂直的性质定理可得:PO⊥平面ABCD.于是VM-OPB=$\frac{1}{2}{V}_{P-OBC}$,即可得出.
解答 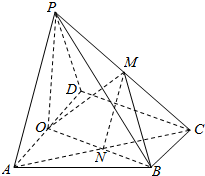 (1)证明:∵CD⊥AD,
(1)证明:∵CD⊥AD,
平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,
∴CD⊥底面PAD.
(2)证明:连接AC交OB于点N,连接MN.
∵BC∥AO,BC=AO,
∴AN=NC.
∵PA∥平面MOB,平面PAC∩平面OMB=MN,
∴AP∥MN,又AN=NC.
∴PM=MC.
(3)解:∵PA=PD=2=AD,OA=OD,
∴PO⊥AD.
∵平面PAD⊥底面ABCD,平面PAD∩底面ABCD=AD,
∴PO⊥平面ABCD.
∴VM-OPB=$\frac{1}{2}{V}_{P-OBC}$
=$\frac{1}{2}×\frac{1}{3}{S}_{△OBC}•PO$
=$\frac{1}{6}$×$\frac{1}{2}×\sqrt{3}×1$×$\sqrt{3}$
=$\frac{1}{3}$.
点评 本题考查了空间线面面面的位置关系、三角形中位线定理、平行线的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.函数f(x)=x2对于任意的x,y∈R都有( )
| A. | f(x+y)=f(x)f(y) | B. | f(xy)=f(x)+f(y) | C. | f(xy)=f(x)f(y) | D. | f(x+y)=f(x)+f(y) |
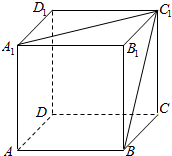 在正方体ABCD-A1B1C1D1中,求:
在正方体ABCD-A1B1C1D1中,求: 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAD=60°,AE⊥BD.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AB=2BC,∠BAD=60°,AE⊥BD.