题目内容
已知A、B、C是三角形的内角, sinA,-cosA是方程x2-x+2a=0的两根.
sinA,-cosA是方程x2-x+2a=0的两根.
(1)求角A;
(2)若 =-3,求tanB.
=-3,求tanB.
解 (1)由已知可得, sinA-cosA=1.①
sinA-cosA=1.①
又sin2A+cos2A=1,∴sin2A+( sinA-1)2=1,
sinA-1)2=1,
即4sin2A-2 sinA=0,
sinA=0,
得sinA=0(舍去)或sinA= .∴A=
.∴A=
将A= 代入①知A=
代入①知A= π时不成立,
π时不成立,
∴A= .
.
(2)
得sin2B-sinBcosB-2cos2B=0.
∵cosB≠0,∴tan2B-tanB-2=0,
∴tanB=2或tanB=-1.
∵tanB=-1使cos2B-sin2B=0,舍去.
故tanB=2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
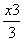 +x2-3x-4在[0,2]上的最小值是( )
+x2-3x-4在[0,2]上的最小值是( )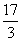 B.-
B.-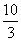
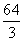
 ,则sinα=( )
,则sinα=( ) B.
B. D.
D. 等于( )
等于( )
 A.
A. B.-
B.- D.-
D.-
 )=
)= ,且-
,且- <α<0,则
<α<0,则 等于( )
等于( ) B.-
B.-
 D.
D.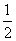 (sinx+cosx)-
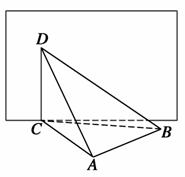
(sinx+cosx)- m,在A处看到着火点的仰角为60°,∠ABC=30°,∠BAC=105°,求两支水枪的喷射距离至少是多少?
m,在A处看到着火点的仰角为60°,∠ABC=30°,∠BAC=105°,求两支水枪的喷射距离至少是多少?