题目内容
已知函数 .
.
(Ⅰ)若函数 在
在 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;
(Ⅱ)若 ,
, 且
且 ,设
,设 ,求函数
,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
(Ⅰ)解:由题设可得
因为函数 在
在 上是增函数,
上是增函数,
所以,当 时,不等式
时,不等式 即
即 恒成立
恒成立
因为,当 时,
时, 的最大值为
的最大值为 ,则实数
,则实数 的取值范围是
的取值范围是 -----4分
-----4分
(Ⅱ) 解:  ,
,

所以, …………6分
…………6分
(1) 若 ,则
,则 ,在
,在 上, 恒有
上, 恒有 ,
,
所以 在
在 上单调递减
上单调递减
 ,
, …………7分
…………7分
(2)  时
时
(i)若 ,在
,在 上,恒有
上,恒有
所以 在
在 上单调递减
上单调递减

 …………9分
…………9分
ii) 时,因为
时,因为 ,所以
,所以
 ,所以
,所以
所以 在
在 上单调递减
上单调递减

 …………11分
…………11分
综上所述:当 时,
时, ,
, ;当
;当
且 时,
时, ,
, .…………12分
.…………12分

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
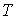 (单位:年)有关.若
(单位:年)有关.若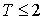 ,则销售利润为
,则销售利润为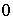 元;若
元;若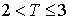 ,则销售利润为
,则销售利润为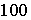 元;若
元;若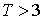 ,则销售利润为
,则销售利润为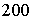 元,设每台该种电器的无故障使用时间
元,设每台该种电器的无故障使用时间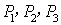 ,又知
,又知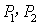 是方程
是方程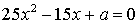 的两个根,且
的两个根,且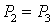 .
.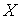 表示销售两台该种电器的销售利润总和,求
表示销售两台该种电器的销售利润总和,求 的四个根组成一个首项为
的四个根组成一个首项为 的等差数列,则
的等差数列,则 ____________.
____________. 的部分图象,则函数
的部分图象,则函数 的零点所在的区间是( )
的零点所在的区间是( ) B.
B. C.
C. D.
D.

 是减函数,且函数
是减函数,且函数 的图象关于(1,0)成中心对称,若
的图象关于(1,0)成中心对称,若 满足不等式
满足不等式 ,则当
,则当 时,
时, 的取值范围是 .
的取值范围是 .  恒成立,则不等式
恒成立,则不等式 的解集是( )
的解集是( ) 上,
上, 为曲线在点P处的切线的倾斜角,则
为曲线在点P处的切线的倾斜角,则 B.
B. C.
C. D.[0,
D.[0, )
) 作为点P的横、纵坐标,则点P在直线
作为点P的横、纵坐标,则点P在直线 上的概率为_________。
上的概率为_________。 }, M∩P=( )
}, M∩P=( ) B.
B.  C.
C.  D.
D. 