题目内容
方程lnx=6-2x的根必定属于区间( )
| A.(-2,1) | B.(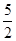 ,4) ,4) | C.(1,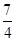 ) ) | D.(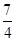 , ,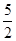 ) ) |
B
解析

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
设计下列函数求值算法程序时需要运用条件语句的函数为( ).
A. |
B. |
C. |
D. |
已知函数 ,且
,且 ,则( )
,则( )
A. | B. | C. | D. |
已知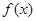 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, ,则函数
,则函数 的零点的集合为( )
的零点的集合为( )
A. | B. | C. | D. |
观察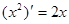 ,
,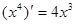 ,
,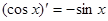 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数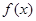 满足
满足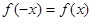 ,记
,记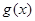 为
为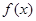 的导函数,则
的导函数,则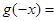 ( )
( )
A.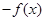 | B.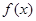 | C.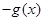 | D.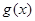 |
已知函数 满足
满足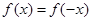 ,且当
,且当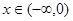 时,
时,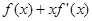
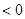 成立, 若
成立, 若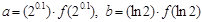 ,
, 的大小关系是( )
的大小关系是( )
A.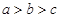 | B.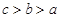 | C.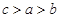 | D.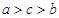 |
函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)( ).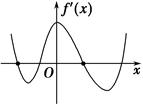
| A.无极大值点,有四个极小值点 |
| B.有三个极大值点,两个极小值点 |
| C.有两个极大值点,两个极小值点 |
| D.有四个极大值点,无极小值点 |
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f(x)=lnx-ax,若函数在定义域上有且仅有4个零点,则实数a的取值范围是( )
| A.(e,+∞) | B.(0, ) ) |
C.(1, ) ) | D.(-∞, ) ) |
[2014·福州质检]设二次函数f(x)=ax2-2ax+c在区间[0,1]上单调递减,且f(m)≤f(0),则实数m的取值范围是( )
| A.(-∞,0] | B.[2,+∞) |
| C.(-∞,0]∪[2,+∞) | D.[0,2] |