题目内容
△ABC中，若A=2B，则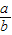
的取值范围是 ．
【答案】分析：先通过正弦定理及A=2B求出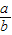
=2cosB，再根据A=2B和三角形内角和为180°求出B的范围，进而根据余弦函数的单调性求出答案．
解答：解：∵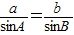
，∴
=
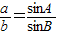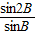=2cosB，
∵A=2B
∴A+B+C=3B+C=180°
∴B=60°-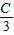
∴B＜60°
又∵B＞0°
∴
＜cosB＜1
∴1＜2cosB＜2
故答案为：（1，2）
点评：本题主要考查了正弦定理的应用．在三角形中解题时要注意角的范围．
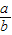=2cosB，再根据A=2B和三角形内角和为180°求出B的范围，进而根据余弦函数的单调性求出答案．解答：解：∵
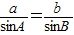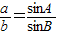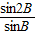，∴==2cosB，∵A=2B
∴A+B+C=3B+C=180°
∴B=60°-
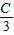
∴B＜60°
又∵B＞0°
∴
＜cosB＜1∴1＜2cosB＜2
故答案为：（1，2）
点评：本题主要考查了正弦定理的应用．在三角形中解题时要注意角的范围．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
在△ABC中，若a=2，b=2
，c=
+
，则A的度数为（ ）
| 2 |
| 6 |
| 2 |
| A、30° | B、45° |
| C、60° | D、75° |