Question

【题目】命题p：函数f（x）= （a＞0，且a≠1）在R上为单调递减函数，命题q：x∈[0， ]，x2﹣a≤0恒成立．
（1）求命题q真时a的取值范围；
（2）若命题p∧q为假，p∨q为真，求a的取值范围．

Answer 1

【答案】
（1）解：若命题q为真命题，

则a≥x2，x∈[0， ]，恒成立，

即a≥x2max，即 ；

（2）解：若函数f（x）= （a＞0，

且a≠1）在R上为单调递减函数，

则 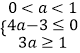，解得： ≤a≤ ；

若命题p∧q为假，p∨q为真，

则命题p，q一真一假，

当p真q假时，a＜ 且 ≤a≤ ，解得： ；

当p假q真时，a≤0，或a≥1，且 ，解得： ；

综上可得： 或 ．

【解析】（1）若命题q为真命题，则a≥x2 ， x∈[0， ]，恒成立，即a≥x2max；（2）若命题p∧q为假，p∨q为真，命题p，q一真一假，进而可得满足条件的a的取值范围．
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案，需要熟知两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．