题目内容
直线l1:2x-3y+4=0关于直线x-y=0的对称直线l2的方程为
3x-2y-4=0.
3x-2y-4=0.
.分析:利用到角公式求出对称直线的斜率,求出已知直线的交点坐标,利用点斜式求出直线l2的方程.
解答:解:设直线l2的斜率为k,直线y=x的斜率为1,直线l1:2x-3y+4=0的斜率为
,
因为直线l1:2x-3y+4=0关于直线x-y=0的对称直线l2,
所以直线l1到直线x-y=0的角与直线x-y=0到直线l2的角相等.
所以
=
,k=
,
由2x-3y+4=0与x-y=0的交点坐标为(4,4)
所求对称直线方程为:y-4=
(x-4),
所求直线方程为:3x-2y-4=0.
故答案为:3x-2y-4=0.
| 2 |
| 3 |
因为直线l1:2x-3y+4=0关于直线x-y=0的对称直线l2,
所以直线l1到直线x-y=0的角与直线x-y=0到直线l2的角相等.
所以
1-
| ||
1+1×
|
| k-1 |
| 1+k |
| 3 |
| 2 |
由2x-3y+4=0与x-y=0的交点坐标为(4,4)
所求对称直线方程为:y-4=
| 3 |
| 2 |
所求直线方程为:3x-2y-4=0.
故答案为:3x-2y-4=0.
点评:本题考查求点关于直线的对称点的坐标的方法,考查到角公式的应用,也可以利用轨迹方程的求法求解本题,方法比较多.

练习册系列答案
相关题目
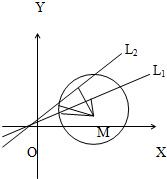 如图,已知两条直线L1:2x-3y+2=0,L2:3x-2y+3=0.有一动圆(圆心和半径都在变动)与L1,L2都相交,并且L1,L2被截在圆内的两条线段的长度分别是定值26,24,求圆心M的轨迹方程,并说出轨迹的名称.
如图,已知两条直线L1:2x-3y+2=0,L2:3x-2y+3=0.有一动圆(圆心和半径都在变动)与L1,L2都相交,并且L1,L2被截在圆内的两条线段的长度分别是定值26,24,求圆心M的轨迹方程,并说出轨迹的名称.