题目内容
在△ABC中,已知cos A=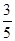 .
.
(1)求sin2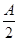 -cos(B+C)的值;
-cos(B+C)的值;
(2)若△ABC的面积为4,AB=2,求BC的长.
(1) .(2) BC=
.(2) BC= .
.
解析试题分析:(1)sin2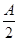 -cos(B+C)=
-cos(B+C)= +cos A=
+cos A= +
+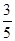 =
= . 5分
. 5分
(2)在△ABC中,∵cos A=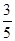 ,∴sin A=
,∴sin A= .
.
由S△ABC=4,得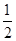 bcsin A=4,得bc=10.∵c=AB=2,∴b=5.
bcsin A=4,得bc=10.∵c=AB=2,∴b=5.
∴BC2=a2=b2+c2-2bccos A=52+22-2×5×2×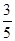 =17.∴BC=
=17.∴BC= . 10分
. 10分
考点:本题考查了三角恒等变换及余弦定理的运用
点评:已知三角形的三个独立条件(不含已知三个角的情况),应用两定理,可以解三角形

练习册系列答案
相关题目
 的两个根, 且
的两个根, 且 。求:(1)角C的度数; (2)AB的长度。
。求:(1)角C的度数; (2)AB的长度。 处,发现北偏东
处,发现北偏东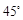 方向,距
方向,距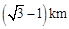 的
的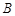 处有一艘走私船,在
处有一艘走私船,在 方向,距
方向,距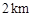 的
的 处的缉私船奉命以
处的缉私船奉命以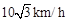 的速度追截走私船,此时走私船正以
的速度追截走私船,此时走私船正以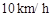 的速度从
的速度从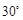 方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (
方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间. (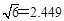 )
)
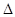 ABC中,
ABC中, 所对边分别为
所对边分别为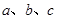 ,且满足
,且满足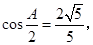
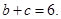
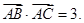
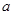 的值;
的值;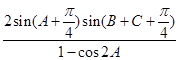 的值.
的值.  ,且c =
,且c = ,C =
,C =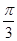 ,求a,b的值
,求a,b的值 中,已知
中,已知


 求A的值.
求A的值.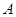 、
、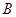 、
、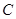 为
为 的三个内角,且其对边分别为
的三个内角,且其对边分别为 、
、 、
、 ,若
,若 .
. ,求
,求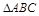 中,
中,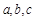 分别是角
分别是角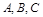 的对边,
的对边, ,
, .
. 的值;
的值; ,求边
,求边 的长.
的长.