题目内容
已知点P是△ABC的内心（三个内角平分线交点）、外心（三条边的中垂线交点）、重心（三条中线交点）、垂心（三个高的交点）之一，且满足2
•
=
2-
2，则点P一定是△ABC的（ ）
| AP |
| BC |
| AC |
| AB |
分析：设D为BC的中点，可得
+
=2
．根据向量数量积的运算性质，将2
•
=
2-
2化简，得到2
•（
-
）=0，从而得到
•
=0，即
⊥
，从而得到P在BC的垂直平分线上．由此根据三角形外心的性质，结合题意可得答案．
| AC |
| AB |
| AD |
| AP |
| BC |
| AC |
| AB |
| BC |
| AD |
| AP |
| BC |
| PD |
| BC |
| PD |
解答：解：设D为BC的中点，可得
+
=2
∵
2-
2=(
+
)(
-
)
∴点P满足2
•
=
2-
2=2
•（
-
）
∵向量
=
-
∴2
•
=2
•
，移项得2
•（
-
）=0
即
•
=0，得
⊥
．结合D为BC的中点，可得P在BC的垂直平分线上
又∵点P是△ABC的内心、外心、重心和垂心之一
∴结合三角形外接圆的性质，得点P是△ABC的外心
故选：B
| AC |
| AB |
| AD |
∵
| AC |
| AB |
| AC |
| AB |
| AC |
| AB |
∴点P满足2
| AP |
| BC |
| AC |
| AB |
| AD |
| AC |
| AB |
∵向量
| BC |
| AC |
| AB |
∴2
| AP |
| BC |
| AD |
| BC |
| BC |
| AD |
| AP |
即
| BC |
| PD |
| BC |
| PD |
又∵点P是△ABC的内心、外心、重心和垂心之一
∴结合三角形外接圆的性质，得点P是△ABC的外心
故选：B
点评：本题给出三角形中的点P满足的向量等式，求点P是三角形四心中的哪一个．着重考查了向量的线性运算法则、向量的数量积及其运算性质和三角形的四心等知识，属于中档题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
．设△ABC，△PBC，△PCA，△PAB的面积分别为S，S1，S2，S3，记
，
，
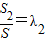．则λ2•λ3取最大值时，2x+y的值为（ ）
