题目内容
已知函数 ,
, .
.
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若方程 仅有一个实根,求实数
仅有一个实根,求实数 的取值集合.
的取值集合.
(1)单调递增区间为 ,不存在单调递减区间;(2)
,不存在单调递减区间;(2) 或
或 ;
;
【解析】
试题分析:(1)由题可知,将 代入,可得
代入,可得 ,由于真数x(x+1)>0,可知x(x+1)在定义域上始终递增,外层对数函数始终递增,即单调递增区间为
,由于真数x(x+1)>0,可知x(x+1)在定义域上始终递增,外层对数函数始终递增,即单调递增区间为 ,不存在单调递减区间;(2)由题可知,由
,不存在单调递减区间;(2)由题可知,由 ,即
,即 ,根据真数大于0,真数相等,可列出不等式组,对k进行讨论,即可得出k的取值;
,根据真数大于0,真数相等,可列出不等式组,对k进行讨论,即可得出k的取值;
试题解析:(Ⅰ)当 时,
时, (其中
(其中 ),由复合函数单调性可知内层函数x(x+1)在定义域上始终递增,外层对数函数始终递增,所以,
),由复合函数单调性可知内层函数x(x+1)在定义域上始终递增,外层对数函数始终递增,所以, 的单调递增区间为
的单调递增区间为 ,不存在单调递减区间;
,不存在单调递减区间;
(Ⅱ)由 ,即
,即 .该方程可化为不等式组
.该方程可化为不等式组 
(1)若 时,则
时,则 ,原问题即为:方程
,原问题即为:方程 在
在 上有根,解得
上有根,解得 ;
;
(2)若 时,则
时,则 ,原问题即为:方程
,原问题即为:方程 在
在 上有根,解得
上有根,解得 .综上可得
.综上可得 或
或 为所求.
为所求.
考点:①复合函数的单调性②对数函数单调性的应用

练习册系列答案
相关题目
 的实数根个数为 .
的实数根个数为 .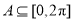 ,集合
,集合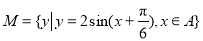 ,若
,若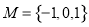 ,则不同集合A的个数是
,则不同集合A的个数是 表示平面区域为
表示平面区域为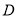 ,在区域
,在区域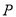 ,则点
,则点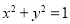 内的概率为 .
内的概率为 .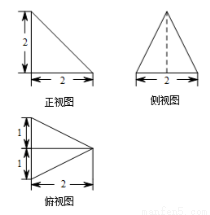
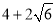 B.
B.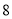 C.
C.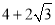 D.
D.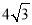
 、
、 满足:对任意
满足:对任意 有
有
 且
且 .若
.若 ,则
,则 .
. ,
, ,
, ,由
,由 的大小关系为( )
的大小关系为( )  B.
B. C.
C. D.
D.
 的周长是
的周长是 ,且
,且 ,则顶点
,则顶点 的轨迹方程是
的轨迹方程是


 K]
K] 与
与 的等比中项为 .
的等比中项为 .