设向量,,则下列结论中正确的是( )A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

设向量,,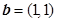则下列结论中正确的是（　　）

A．

B．

C．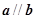

D．

解析试题分析：因为那么可知根据向量共线的充要条件得到12-010,故不共线。选项C错误，且，选项D错误，
且由向量的数量积公式可知，故选择B错误，
而

故选项A正确，选A
考点：本试题主要考查了向量共线的充要条件、考查向量垂直的充要条件
点评：解决该试题的关键运用公式判定垂直，运用判定平行。

练习册系列答案

同步解析与测评初中总复习指导与训练系列答案

相关题目

与向量的夹角相等，且模为1的向量是 ( )

A．	B．或
C．	D．或

在△ABC中，M是的中点，＝1，点在上且满足＝2，则·(＋)等于（　　　）

已知，满足：，，，则 ( )

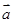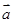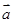已知向量=" (1,2" ), =" (2,-3" )，若向量满足(+)//,⊥(+),则=（）

A．(,)	B．(-,-)
C．(,)	D．(-,-)

已知平面向量与的夹角为60^o，且满足，若=1，则＝（）

设为两个不共线向量，若，其中为实数，则记．已知两个非零向量满足，则下述四个论断中正确的序号为______．（所有正确序号都填上）
①； ②，其中；
③∥； ④⊥．

已知向量( )

已知向量，若则

试题分类