题目内容
已知向量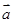 =" (1,2" ),
=" (1,2" ),  =" (2,-3" ),若向量
=" (2,-3" ),若向量 满足(
满足( +
+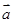 )//
)// ,
, ⊥(
⊥(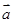 +
+ ),则
),则 =( )
=( )
A.( , , ) ) | B.(- ,- ,- ) ) |
C.( , , ) ) | D.(- ,- ,- ) ) |
D
解析试题分析:由题意可知,设向量 =" (x,y" ),向量
=" (x,y" ),向量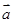 =" (1,2" ),
=" (1,2" ),  =" (2,-3" ),那么由(
=" (2,-3" ),那么由( +
+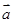 )//
)// ,可知有(1+x,2+y)//(2,-3),则得到3(1+x)-2(2+y)=0,3x-2y-1=0,又因为
,可知有(1+x,2+y)//(2,-3),则得到3(1+x)-2(2+y)=0,3x-2y-1=0,又因为 ⊥(
⊥(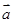 +
+ ),那么即为(x,y ).(3,-1)=0,3x-y=0,联立方程组得到x=-
),那么即为(x,y ).(3,-1)=0,3x-y=0,联立方程组得到x=- ,y=-
,y=- ,选D.
,选D.
考点:本试题主要考查了向量的共线问题,以及向量的垂直的证明运用。
点评:解决该试题的关键是利用向量的坐标运算表示出和向量的坐标,并根据垂直时数量积为零得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以下说法错误的是 ( )
A.直角坐标平面内直线的倾斜角的取值范围是 |
B.直角坐标平面内两条直线夹角的取值范围是 |
C.平面内两个非零向量的夹角的取值范围是 |
D.空间两条直线所成角的取值范围是 |
若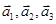 均为单位向量,则“
均为单位向量,则“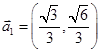 ”是“
”是“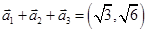 ”的(
”的( 条件。
条件。
| A.充分非必要 | B.必要非充分 | C.既不充分也不必要 | D.充要 |
已知 为等腰三角形,
为等腰三角形, ,
, 为
为 边上的高,若
边上的高,若
 ,
,
 ,则
,则 ( )
( )
A. | B. |
C.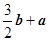 | D. |
已知向量 ,且
,且 ,则实数
,则实数 等于( )
等于( )
A. | B. | C. | D. |
设向量 ,
,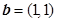 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C.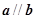 | D. |
已知向量 ,
, ,且
,且 ,那么
,那么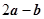 等于( )
等于( )
A. | B. | C.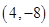 | D. |
已知 =(3,1),
=(3,1), =(
=( ,5)则3
,5)则3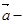 2
2 = ( )
= ( )
| A.(2,7) | B.(13, ) ) | C.(2, ) ) | D.(13,13) |