题目内容
在△ABC中,M是 的中点,
的中点, =1,点
=1,点 在
在 上且满足
上且满足 =2
=2 ,则
,则 ·(
·( +
+ )等于( )
)等于( )
A.- | B.- | C. | D. |
A
解析试题分析:由题意可知, 是
是 边上的中线,因为点
边上的中线,因为点 在
在 上且满足
上且满足 =2
=2 ,所以
,所以 ·(
·( +
+ )
)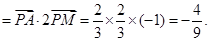
考点:本小题主要考查平面向量的线性运算、向量加法的平行四边形法则的应用和平面向量的数量积运算,考查学生数形结合思想的应用.
点评:本小题解题的关键在于看出 +
+ 等于
等于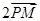 .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
设 ,
, ,
, 为坐标平面上三点,
为坐标平面上三点, 为坐标原点,若
为坐标原点,若 与
与 在
在 方向上的投影相同,则
方向上的投影相同,则 与
与 满足的关系式为( )
满足的关系式为( )
A. | B. | C. | D. |
已知 ,
, ,则下列结论正确的是
,则下列结论正确的是
A. ∥ ∥  | B. |
C. 与 与 垂直 垂直 | D. 与 与 的夹角为 的夹角为 |
若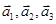 均为单位向量,则“
均为单位向量,则“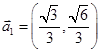 ”是“
”是“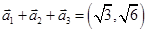 ”的(
”的( 条件。
条件。
| A.充分非必要 | B.必要非充分 | C.既不充分也不必要 | D.充要 |
如图,四面体ABCD中,点E是CD的中点,记 ,
,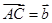 ,
, ,则
,则 =
=
A.    + +  | B.  + +  + +  |
C.    + +  | D.   + + + +  |
已知 为等腰三角形,
为等腰三角形, ,
, 为
为 边上的高,若
边上的高,若
 ,
,
 ,则
,则 ( )
( )
A. | B. |
C.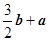 | D. |
设向量 ,
,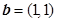 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. | B. | C.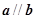 | D. |
设向量
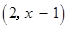 ,
,
 ,则“
,则“ ”是“
”是“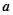 //
// ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知向量 ,
, ,若
,若 ∥
∥ ,则
,则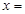 ( )
( )
A. | B. | C. | D. |