题目内容
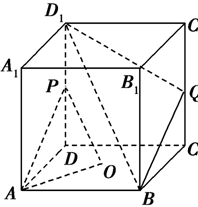
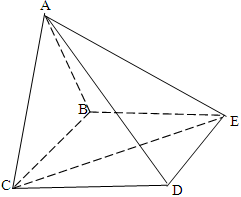
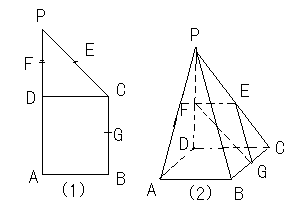
(本题满分14分)如图,四棱锥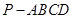 的底面
的底面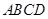 为矩形,且
为矩形,且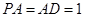 ,
,
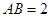 ,
,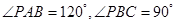 ,
,
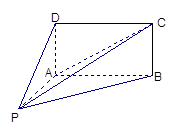
(Ⅰ)平面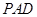 与平面
与平面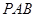 是否垂直?并说明理由;
是否垂直?并说明理由;
(Ⅱ)求直线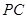 与平面
与平面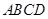 所成角的正弦值.
所成角的正弦值.
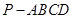 的底面
的底面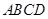 为矩形,且
为矩形,且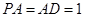 ,
,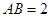 ,
,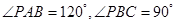 ,
,
(Ⅰ)平面
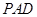 与平面
与平面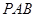 是否垂直?并说明理由;
是否垂直?并说明理由;(Ⅱ)求直线
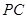 与平面
与平面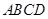 所成角的正弦值.
所成角的正弦值. (I)见解析;(Ⅱ) .
.
 .
.本试题主要是考查了面面垂直和线面角的求解的综合运用。
(1)第一问中要证明面面垂直关键是证明线面垂直,然后利用判定定理得到。
(2)第二问先根据线面角的定义,作出线面角,然后利用直角三角形的边角的关系求解的得到。

(I)平面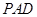
 平面
平面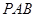 ; …………………1分
; …………………1分
证明:由题意得 且
且
又 ,则
,则 …………………………3分
…………………………3分
则 平面
平面 , ………………5分
, ………………5分
故平面 平面
平面 ………………7分
………………7分
(Ⅱ)解法1:以点A为坐标原点,AB所在的直线为y轴建立
空间直角坐标系如右图示,则 ,
, ,
, 可得
可得 , 9分
, 9分
平面ABCD的单位法向量为 , ……………………………………11分
, ……………………………………11分
设直线PC与平面ABCD所成角为 ,则
,则 13分
13分
则 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值 ……………………………14分
……………………………14分
解法2:

由(I)知 平面
平面 ,∵
,∵ 面
面
∴平面ABCD⊥平面PAB, …………………………9分
在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,
则∠PCE为直线PC与平面ABCD所成的角, …………………………11分
在Rt△PEA中,∵∠PAE=60°,PA=1,∴ ,
,
又
∴ …………………………13分
…………………………13分
在Rt△PEC中 .………………14分
.………………14分
(1)第一问中要证明面面垂直关键是证明线面垂直,然后利用判定定理得到。
(2)第二问先根据线面角的定义,作出线面角,然后利用直角三角形的边角的关系求解的得到。

(I)平面
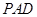
 平面
平面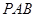 ; …………………1分
; …………………1分证明:由题意得
 且
且
又
 ,则
,则 …………………………3分
…………………………3分则
 平面
平面 , ………………5分
, ………………5分故平面
 平面
平面 ………………7分
………………7分(Ⅱ)解法1:以点A为坐标原点,AB所在的直线为y轴建立
空间直角坐标系如右图示,则
 ,
, ,
, 可得
可得 , 9分
, 9分平面ABCD的单位法向量为
 , ……………………………………11分
, ……………………………………11分设直线PC与平面ABCD所成角为
 ,则
,则 13分
13分则
 ,即直线PC与平面ABCD所成角的正弦值
,即直线PC与平面ABCD所成角的正弦值 ……………………………14分
……………………………14分解法2:

由(I)知
 平面
平面 ,∵
,∵ 面
面
∴平面ABCD⊥平面PAB, …………………………9分
在平面PAB内,过点P作PE⊥AB,垂足为E,则PE⊥平面ABCD,连结EC,
则∠PCE为直线PC与平面ABCD所成的角, …………………………11分
在Rt△PEA中,∵∠PAE=60°,PA=1,∴
 ,
,又

∴
 …………………………13分
…………………………13分在Rt△PEC中
 .………………14分
.………………14分
练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
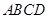 中,
中,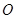 、
、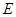 分别是
分别是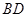 、
、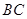 的中点,
的中点,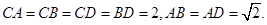
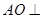 平面
平面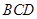 ;
;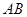 与
与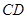 所成角余弦值的大小;
所成角余弦值的大小;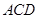 的距离.
的距离.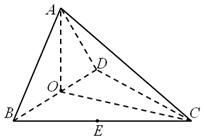
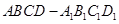 中,
中,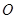 为底面
为底面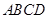 的中心,
的中心,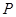 是
是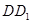 的中点,设
的中点,设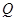 是
是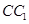 上的中点,求证:(1)
上的中点,求证:(1)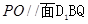 ;
;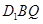 ∥平面
∥平面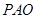 .
.
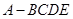 中,底面
中,底面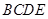 为矩形,侧面
为矩形,侧面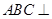 底面
底面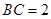 ,
,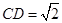 ,
,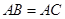 .
.
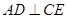 ;
; 与平面
与平面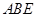 所成的角为
所成的角为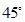 ,
, 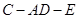 的余弦值.
的余弦值.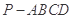 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.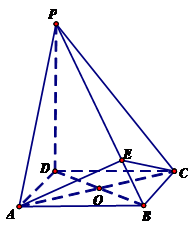
 ;
; 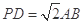 且
且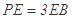 时,求AE与平面PDB所成的角的正切值.
时,求AE与平面PDB所成的角的正切值.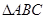 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①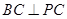 ;②
;②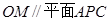 ;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )
;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )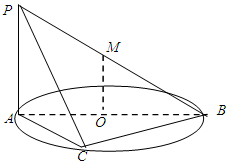
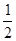 AB=1,M是PB的中点
AB=1,M是PB的中点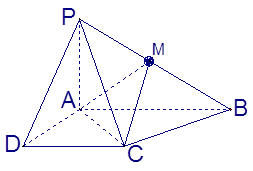
 ,
,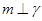 ,那么必有( )
,那么必有( )