题目内容
已知函数 在
在 处取得极小值2.
处取得极小值2.
(1)求函数 的解析式;
的解析式;
(2)求函数 的极值;
的极值;
(3)设函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(1)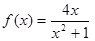
(2)当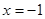 时,函数
时,函数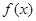 有极小值-2;当
有极小值-2;当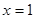 时,函数
时,函数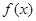 有极大值2
有极大值2
(3)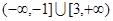
【解析】
试题分析:(1)∵函数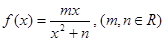 在
在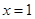 处取得极小值2,
处取得极小值2,
∴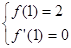 , ……1分
, ……1分
又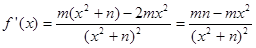 ,
,
∴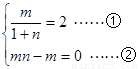
由②式得m=0或n=1,但m=0显然不合题意,
∴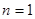 ,代入①式得m=4
,代入①式得m=4
∴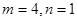 ……2分
……2分
经检验,当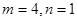 时,函数
时,函数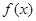 在
在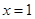 处取得极小值2, ……3分
处取得极小值2, ……3分
∴函数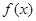 的解析式为
的解析式为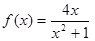 . ……4分
. ……4分
(2)∵函数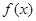 的定义域为
的定义域为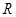 且由(1)有
且由(1)有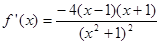 ,
,
令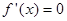 ,解得:
,解得: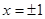 , ……5分
, ……5分
∴当x变化时,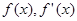 的变化情况如下表:
……7分
的变化情况如下表:
……7分
|
x |
|
-1 |
|
1 |
|
|
|
— |
0 |
+ |
0 |
— |
|
|
减 |
极小值-2 |
增 |
极大值2 |
减 |
∴当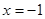 时,函数
时,函数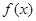 有极小值-2;当
有极小值-2;当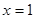 时,函数
时,函数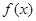 有极大值2, ……8分
有极大值2, ……8分
(3)依题意只需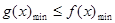 即可.
即可.
∵函数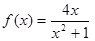 在
在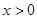 时,
时,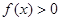 ;在
;在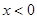 时,
时,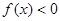 且
且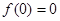 ,
,
∴ 由(2)知函数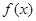 的大致图象如图所示:
的大致图象如图所示:
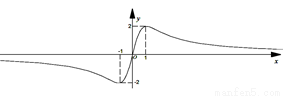
∴当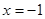 时,函数
时,函数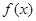 有最小值-2, ……9分
有最小值-2, ……9分
又对任意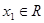 ,总存在
,总存在 ,使得
,使得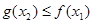 ,
,
∴当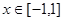 时,
时,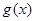 的最小值不大于-2, ……10分
的最小值不大于-2, ……10分
又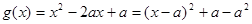
①当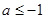 时,
时,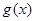 的最小值为
的最小值为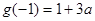 ,
,
∴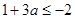 得
得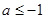 ; ……11分
; ……11分
②当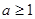 时,
时,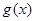 的最小值为
的最小值为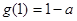
∴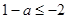 得
得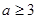 ; ……12分
; ……12分
③当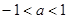 时,
时,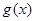 的最小值为
的最小值为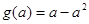
∴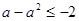 得
得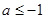 或
或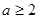
又∵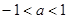
∴此时a不存在, ……13分
综上所述,a的取值范围是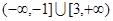 . ……14分
. ……14分
考点:本小题主要考查导数的性质及其应用.
点评:导数是研究函数性质(尤其是单调性、极值、最值等)的有力工具,要灵活应用.求函数的极值时,要先求导数再求极值点,这是最好列出表格,清楚直观,求函数的最值时,一般要涉及到分类讨论,分类讨论时要做到分类标准不重不漏.

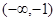
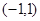
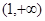
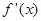
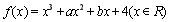
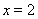
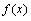

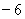



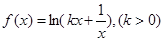 在
在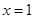 处取得极小值.
处取得极小值. 的值;
的值; 在
在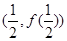 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线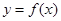 不可能在直线
不可能在直线