题目内容
(本小题满分9分)
已知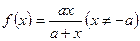 ,且
,且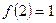 。
。
(Ⅰ)求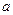 的值;
的值;
(Ⅱ)若在数列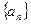 中,
中,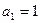 ,
,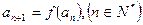 ,计算
,计算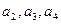 ,并由此猜想通项公式
,并由此猜想通项公式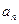 ;
;
(Ⅲ)证明(Ⅱ)中的猜想。
已知
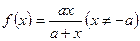 ,且
,且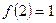 。
。(Ⅰ)求
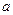 的值;
的值;(Ⅱ)若在数列
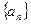 中,
中,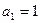 ,
,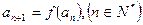 ,计算
,计算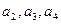 ,并由此猜想通项公式
,并由此猜想通项公式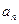 ;
;(Ⅲ)证明(Ⅱ)中的猜想。
解:(Ⅰ)因为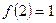 ,所以
,所以 。 ……………………………2分
。 ……………………………2分
(Ⅱ)在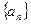 中,因为
中,因为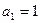 ,
, 。
。
所以 ,
, ,
, ,
,
所以猜想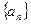 的通项公式为
的通项公式为 。 ………………………6分
。 ………………………6分
(Ⅲ)证明:因为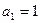 ,
, ,
,
所以 ,即
,即 。
。
所以 是以
是以 为首项,公差为
为首项,公差为 的等差数列。
的等差数列。
所以 ,所以通项公式
,所以通项公式 。 …………………9分
。 …………………9分
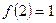 ,所以
,所以 。 ……………………………2分
。 ……………………………2分(Ⅱ)在
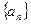 中,因为
中,因为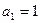 ,
, 。
。所以
 ,
, ,
, ,
,所以猜想
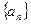 的通项公式为
的通项公式为 。 ………………………6分
。 ………………………6分(Ⅲ)证明:因为
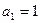 ,
, ,
,所以
 ,即
,即 。
。所以
 是以
是以 为首项,公差为
为首项,公差为 的等差数列。
的等差数列。所以
 ,所以通项公式
,所以通项公式 。 …………………9分
。 …………………9分略

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 在
在 上的单调性,并证明之.
上的单调性,并证明之. 的图像沿x轴向右平移2个单位,所得的图像为C,C关于x轴对称的图像为
的图像沿x轴向右平移2个单位,所得的图像为C,C关于x轴对称的图像为 的图像,则
的图像,则



 件某产品所用的时间(单位:分钟)为
件某产品所用的时间(单位:分钟)为 (A,
(A, 为常数).已知工人组装第4件产品用时30分钟,组装第A件产
为常数).已知工人组装第4件产品用时30分钟,组装第A件产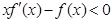 ,对任意正数a,b,若a<b,则必有( )
,对任意正数a,b,若a<b,则必有( )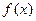 是一次函数,
是一次函数,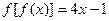 且,则
且,则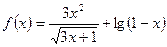 的定义域为____________。
的定义域为____________。 (
( ),定义:当乘积
),定义:当乘积 为整数时,正整数
为整数时,正整数 叫做“理想数”,则区间
叫做“理想数”,则区间 内的所有“理想数”的和为 。
内的所有“理想数”的和为 。 ,函数
,函数 有最小值,则不等式
有最小值,则不等式