题目内容
已知夹在两个平行平面α、β之间的两条斜线段AB=8，CD=12，AB和CD在α内射线长的比为3：5，则α与β的距离为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：首先根据已知条件，建立方程组，进一步求出结果．
解答：
解：设平面α和β间的距离为h，则根据题意：设线段AB在α内的射影长为3x，线段CD在平面α内的射影长为5x．则：
解得：
故选：C
|
解得：
|
故选：C
点评：本题考查的知识要点：平行面间的距离，勾股定理的应用．属于基础题型．
练习册系列答案
相关题目
设等差数列{an}的公差不等于0，且其前n项和为Sn．若2a8=6+a11且a3，a4，a6成等比数列，则S8=（ ）
| A、40 | B、54 | C、80 | D、96 |
已知集合A={0，1，2，3，4}，B={x|x=
，n∈A}，则A∩B的真子集个数为（ ）
| n |
| A、5 | B、6 | C、7 | D、8 |
椭圆两焦点为F1（-4，0）、F2（4，0），P在椭圆上，若△PF1F2的面积的最大值为12，则椭圆方程是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将长、宽分别为4和3的长方形ABCD沿对角线AC折起，得到四面体A-BCD，则四面体A-BCD的外接球的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
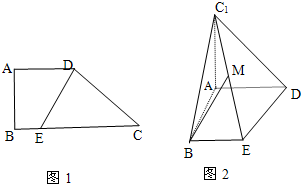如图1，直角梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=