题目内容

求直线y=x-2与曲线x=y2围成图形的面积．
精英家教网
分析：先求出曲线x=y2 和直线y=x-2的交点坐标，从而得到积分的上下限，然后利用定积分表示出图形面积，最后根据定积分的定义求出即可．
解答：解：联立方程解得交点坐标；
A（1，-1），B（4，2）…（4分）
面积S=
∫
1
0
(
x
+
x
)dx+
∫
4
1
(
x
-x+2)dx=
9
2
…（13分）
点评：本题主要考查了定积分在求面积中的应用，以及会利用定积分求图形面积的能力．应用定积分求平面图形面积时，积分变量的选取是至关重要的，属于基础题．
练习册系列答案
相关题目
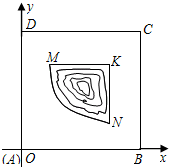如图1，已知抛物线C：y=3x2（x≥0）与直线x=a．直线x=b（其中0≤a≤b）及x轴围成的曲边梯形（阴影部分）的面积可以由公式S=b3-a3来计算，则如图2，过抛物线C：y=3x2（x≥0）上一点A（点A在y轴和直线x=2之间）的切线为l，S1是抛物线y=3x2与切线l及直线y=0所围成图形的面积，S2是抛物线y=3x2与切线l及直线x=2所围成图形的面积，求面积s1+s2的最小值．
精英家教网
（2011•徐州模拟）如图，某新建小区有一片边长为1（单位：百米）的正方形剩余地块ABCD，中间部分MNK是一片池塘，池塘的边缘曲线段MN为函数y=
2
9x
(
1
3
≤x≤
2
3
)的图象，另外的边缘是平行于正方形两边的直线段．为了美化该地块，计划修一条穿越该地块的直路（宽度不计），直路l与曲线段MN相切（切点记为P），并把该地块分为两部分．记点P到边AD距离为t，f（t）表示该地块在直路左下部分的面积．
（1）求f（t）的解析式；
（2）求面积S=f（t）的最大值．
（2012•莆田模拟）如图，边长为3（百米）的正方形ABCD是一个观光区的平面示意图，中间叶形阴影部分MN是一片人工湖，它的左下方边缘曲线段MN为函数y=
2x
(1≤x≤2)的图象．为了便于游客观光，拟在观光区内铺设一条穿越该区域的直路l（宽度不计），其与人工湖左下方曲线段MN相切（切点记为P），并把该区域分为两部分．现直路l左下部分区域规划为花圃，记点P到边AD距离为t，f（t）表示花圃的面积．
（1）求直路l所在的直线与两坐标轴的交点坐标；
（2）求面积f（t）的解析式；
（3）请你制定一个铺设方案，使得花圃面积最大，并求出最大值．

已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点A (0，)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．

    （1）求双曲线C的方程；

    （2）若Q是双曲线线C上的任一点，F1，F2为双曲线C的左、右两个焦点，从F1引∠F1QF2的平分线的垂线，垂足为N，试求点N的轨迹方程；

    （3）设直线y = mx + 1与双曲线C的左支交于A、B两点，另一直线l经过M (–2，0)及AB的中点，求直线l在y轴上的截距b的取值范围．
已知二次函数y=x2，现取x轴上的点，分别为A1(1，0)，A2(2，0)，A3(3，0)，…，An(n，0)，…，过这些点分别作x轴垂线，与抛物线分别交于A′1，A′2，A′3，…，A′n…，记由线段A′nAn，AnAn+1，An+1A′n+1及抛物线弧A′n+1A′n所围成的曲边梯形的面积为an，
(Ⅰ)求数列{an}的通项公式；
(Ⅱ)作直线y=与A′nAn(n =1，2，3，…)交于Bn，记新的曲边梯形A′nBnBn+1A′n+1，面积为bn，求的前n项和Sn；
(Ⅲ)在(Ⅱ)的前提下，作直线y=x，与A′nAn(n=1，2，3，…)交于Cn，记Rt△Cn+1An+1An面积与曲边梯形A′nBnBn+1A′n+1面积之比为Pn，求证：P1+。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网