��Ŀ����
��֪���κ���y=x2����ȡx���ϵĵ㣬�ֱ�ΪA1(1��0)��A2(2��0)��A3(3��0)������An(n��0)����������Щ��ֱ���x�ᴹ�ߣ��������߷ֱ���A��1��A��2��A��3������A��n���������߶�A��nAn��AnAn+1��An+1A��n+1��������A��n+1A��n��Χ�ɵ��������ε����Ϊan��
(��)������{an}��ͨ�ʽ��
(��)��ֱ��y= ��A��nAn(n =1��2��3����)����Bn�����µ���������A��nBnBn+1A��n+1�����Ϊbn����
��A��nAn(n =1��2��3����)����Bn�����µ���������A��nBnBn+1A��n+1�����Ϊbn���� ��ǰn���Sn��
��ǰn���Sn��
(��)��(��)��ǰ���£���ֱ��y=x����A��nAn(n=1��2��3����)����Cn����Rt��Cn+1An+1An�������������A��nBnBn+1A��n+1���֮��ΪPn����֤��P1+ ��
��
(��)������{an}��ͨ�ʽ��
(��)��ֱ��y=
 ��A��nAn(n =1��2��3����)����Bn�����µ���������A��nBnBn+1A��n+1�����Ϊbn����
��A��nAn(n =1��2��3����)����Bn�����µ���������A��nBnBn+1A��n+1�����Ϊbn���� ��ǰn���Sn��
��ǰn���Sn��(��)��(��)��ǰ���£���ֱ��y=x����A��nAn(n=1��2��3����)����Cn����Rt��Cn+1An+1An�������������A��nBnBn+1A��n+1���֮��ΪPn����֤��P1+
 ��
�� 
�⣺(��)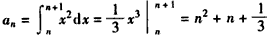 ��
��
(��)�����⣬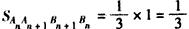 ��
��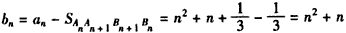 ��
��
��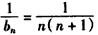 ��
��
��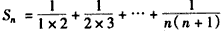
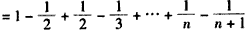 ��
��
��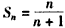 ��
��
(��)��ֱ��������Cn+1An+1An���Ϊdn��
��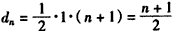 ��
��
��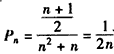 ��
��
��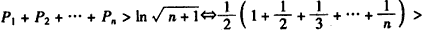
 ��
��
ԭʽ��֤��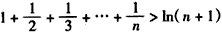 ��
��
����ѧ���ɷ�֤����
�ٵ�n=1ʱ�����=1���ұ�=lna����ߣ��ұߣ����������
�ڼ���n=k��k��1��k��N*��ʱ�����������
��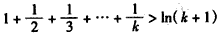 ��
��
��n=k+1ʱ��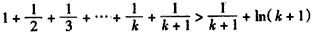 ��
��
��֤��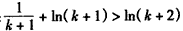
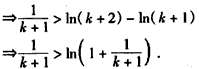
���캯��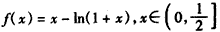 ��
��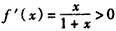 ����f��x����
����f��x����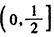 ����������
����������
���Ե�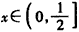 ʱ��
ʱ��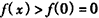 ����x��ln��1+x����
����x��ln��1+x����
��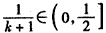 ��
��
��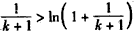 ��
��
�������n=k+1ʱҲ������
�ɢ٢ڵã�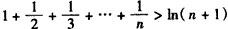 ������n��N*����������ԭ���������
������n��N*����������ԭ���������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ