题目内容
(1)若
=2,求sinα•cosα;
(2)已知sinα是方程2x2-7x+3=0的根,求
.
| sinα+cosα |
| sinα-cosα |
(2)已知sinα是方程2x2-7x+3=0的根,求
tan(π+α)sin(2π-α)cos(
| ||
| cos(π-α)sin(-π-α)tan(π-α) |
分析:(1)把原式去分母,两边平方,化简即可求出
(2)先解方程求出sinα,再由诱导公式对已知式子进行化简,结合同角平方关系可求
(2)先解方程求出sinα,再由诱导公式对已知式子进行化简,结合同角平方关系可求
解答:解:(1)由已知得:sinα+cosα=2(sinα-cosα),
平方得:1+2sinαcosα=4-8sinαcosα,
∴sinαcosα=
(2)∵2x2-7x+3=0的两根是
或3
∴sinα=
=
=tanα
当α为第一象限时,cosα=
,tanα=
当α为第二象限时,cosα=-
,tanα=-
平方得:1+2sinαcosα=4-8sinαcosα,
∴sinαcosα=
| 3 |
| 10 |
(2)∵2x2-7x+3=0的两根是
| 1 |
| 2 |
∴sinα=
| 1 |
| 2 |
tan(π+α)sin(2π-α)cos(
| ||
| cos(π-α)sin(-π-α)tan(π-α) |
| tanα(-sinα)(-sinα) |
| -cosαsinα(-tanα) |
当α为第一象限时,cosα=
| ||
| 2 |
| ||
| 3 |
当α为第二象限时,cosα=-
| ||
| 2 |
| ||
| 3 |
点评:考查学生会进行三角函数中的恒等变换,灵活运用同角三角函数间的基本关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
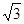 ,且c =
,且c =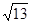 ,C =
,C =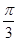 ,求a,b的值
,求a,b的值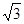 ,且c =
,且c =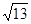 ,C =
,C =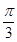 ,求a,b的值.
,求a,b的值.