题目内容
如图,四棱锥 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 .
.
(1)证明:平面 平面
平面 ;
;
(2)若二面角 为
为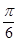 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)证明过程详见解析;(2)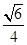 .
.
解析试题分析:(1)可以遵循思路面面垂直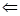 线面垂直
线面垂直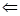 线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明
线线垂直,即证明面面垂直只需要证明其中一个面里面的一条直线垂直与另外一个面即可,即证明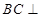 面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即
面PDB,线面垂直只需要证明BC与面内相交的两条直线垂直即可,即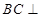 BD,
BD, 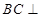 PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
PD,前者可有三角形的勾股定理证得,后者由线面垂直得到
(2)求线面夹角可以利用三维空间直角坐标系,分别以DA,DB,PD三条两两垂直的直线建立坐标系,求面法向量与直线的夹角的余弦值的绝对值即为线面夹角的余弦值.
试题解析:
(1)∵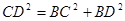 ∴
∴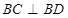
又∵ ⊥底面
⊥底面 ∴
∴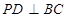
又∵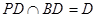 ∴
∴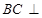 平面
平面
而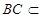 平面
平面 ∴平面
∴平面 平面
平面 5分
5分
(1)由(1)所证,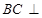 平面
平面 ,所以∠
,所以∠ 即为二面角P-BC-D的平面角,即∠
即为二面角P-BC-D的平面角,即∠
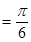
而 ,所以
,所以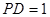 7分
7分
分别以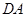 、
、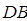 、
、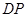 为
为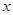 轴、
轴、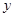 轴、
轴、 轴建立空间直角坐标系.则
轴建立空间直角坐标系.则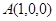 ,
,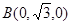 ,
,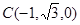 ,
, 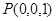 ,所以,
,所以,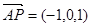 ,
,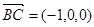 ,
,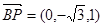 ,设平面
,设平面 的法向量为
的法向量为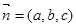 ,则
,则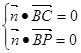 ,即
,即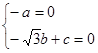 可解得
可解得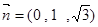 ∴
∴ 与平面
与平面 所成角的正弦值为
所成角的正弦值为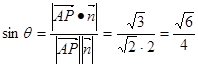 12分
12分
考点:面面垂直 线面夹角

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.
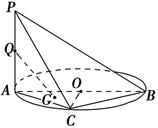
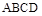 与
与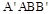 都是边长为
都是边长为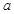 的正方形,点E是
的正方形,点E是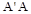 的中点,
的中点,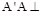 平面
平面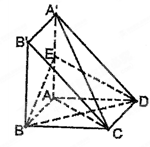
 平面
平面 ;
;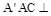 平面
平面 中,点
中,点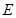 为边
为边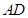 上的点,点
上的点,点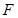 为边
为边 的中点,
的中点, ,现将
,现将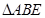 沿
沿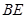 边折至
边折至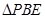 位置,且平面
位置,且平面 平面
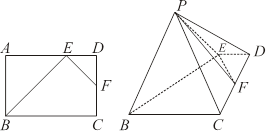
平面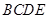 .
.
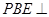 平面
平面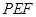 ;
;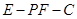 的大小.
的大小.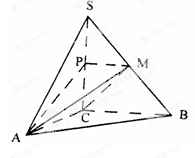
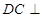 平面
平面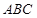 ,
,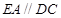 ,
,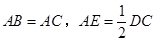 ,
, 为
为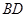 的中点.
的中点.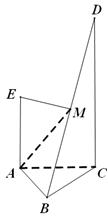
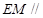 平面
平面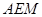
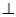 平面
平面 .
.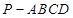 中,
中, 是正方形,
是正方形,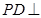 平面
平面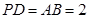 ,
,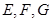 分别是
分别是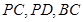 的中点.
的中点.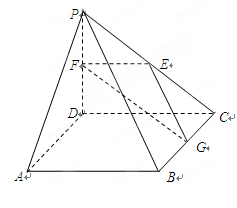
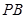 上确定一点
上确定一点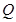 ,使
,使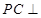 平面
平面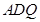 ,并给出证明;
,并给出证明; 平面
平面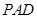 ,并求出
,并求出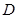 到平面
到平面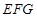 的距离.
的距离. 、
、 、
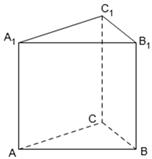
、 为不在同一直线上的三点,且
为不在同一直线上的三点,且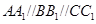 ,
,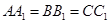 .
.
 //平面
//平面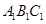 ;
;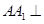 平面
平面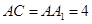 ,
,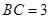 ,
,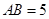 ,求证:
,求证: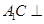 平面
平面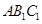 ;
;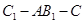 的余弦值.
的余弦值.