题目内容
已知函数 ,其图象过点(
,其图象过点( ,
, ).
).
(1)求φ的值及y=f(x)最小正周期;
(2)将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数y=g(x)的图象,求函数PF2在[0,
,纵坐标不变,得到函数y=g(x)的图象,求函数PF2在[0, ]上的最大值和最小值.
]上的最大值和最小值.
解:(1)∵函数 ,
,
∴f(x)= sin2xsin∅+
sin2xsin∅+ -
- cos∅=
cos∅= sin2xsin∅+
sin2xsin∅+ cos2xcos∅
cos2xcos∅
= ,又函数的图象经过(
,又函数的图象经过( ,
, ),∴
),∴ =
= cos(
cos( -∅),∴cos(
-∅),∴cos( -∅)=1.
-∅)=1.
∵0<∅<π,∴∅= ,故最小正周期等于
,故最小正周期等于  =π.
=π.
(2)由(Ⅰ)知f(x)= ,将函数y=f(x)的图象上各点的横坐标缩短到原来的
,将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,
,
纵坐标不变,得到函数y=g(x)的图象,可知 ,
,
因为 ,
, ,故
,故 .
.
所以y=g(x)在 上的最大值和最小值分别为
上的最大值和最小值分别为 和
和 .
.
分析:(1)由题意可得,f(x)= ,又函数的图象经过(
,又函数的图象经过( ,
, ),可得 cos(
),可得 cos( -∅)=1,据
-∅)=1,据
0<∅<π,得∅= ,故最小正周期等于
,故最小正周期等于  =π.
=π.
(2)由(Ⅰ)知f(x)= ,根据图象的变换可得
,根据图象的变换可得  ,因为
,因为 ,
, ,故
,故 ,从而得到函数在[0,
,从而得到函数在[0, ]上的最大值和最小值.
]上的最大值和最小值.
点评:本题考查三角恒等变换,余弦函数的周期性,余弦函数的定义域和值域,余弦函数的图象变换,得到可知 ,是解题的难点.
,是解题的难点.
 ,
,∴f(x)=
 sin2xsin∅+
sin2xsin∅+ -
- cos∅=
cos∅= sin2xsin∅+
sin2xsin∅+ cos2xcos∅
cos2xcos∅=
 ,又函数的图象经过(
,又函数的图象经过( ,
, ),∴
),∴ =
= cos(
cos( -∅),∴cos(
-∅),∴cos( -∅)=1.
-∅)=1.∵0<∅<π,∴∅=
 ,故最小正周期等于
,故最小正周期等于  =π.
=π.(2)由(Ⅰ)知f(x)=
 ,将函数y=f(x)的图象上各点的横坐标缩短到原来的
,将函数y=f(x)的图象上各点的横坐标缩短到原来的 ,
,纵坐标不变,得到函数y=g(x)的图象,可知
 ,
,因为
 ,
, ,故
,故 .
.所以y=g(x)在
 上的最大值和最小值分别为
上的最大值和最小值分别为 和
和 .
.分析:(1)由题意可得,f(x)=
 ,又函数的图象经过(
,又函数的图象经过( ,
, ),可得 cos(
),可得 cos( -∅)=1,据
-∅)=1,据 0<∅<π,得∅=
 ,故最小正周期等于
,故最小正周期等于  =π.
=π.(2)由(Ⅰ)知f(x)=
 ,根据图象的变换可得
,根据图象的变换可得  ,因为
,因为 ,
, ,故
,故 ,从而得到函数在[0,
,从而得到函数在[0, ]上的最大值和最小值.
]上的最大值和最小值.点评:本题考查三角恒等变换,余弦函数的周期性,余弦函数的定义域和值域,余弦函数的图象变换,得到可知
 ,是解题的难点.
,是解题的难点. 
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,其图象过点
,其图象过点
 的值;
的值; 图象上各点向左平移
图象上各点向左平移 个单位长度,得到函数
个单位长度,得到函数 的图象,求函数
的图象,求函数 在
在 上的单调递增区间.
上的单调递增区间. ,其图象过点
,其图象过点
 的值;
的值; 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值。
上的最大值和最小值。
 ,其图象过点(
,其图象过点( ,
, ).
). 的值及
的值及 最小正周期;
最小正周期; 的图象,求函数
的图象,求函数 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.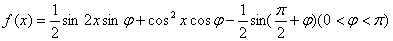 ,其图象过点
,其图象过点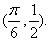
 的值;
的值;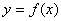 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的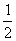 ,纵坐标不变,得到函数
,纵坐标不变,得到函数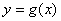 的图象,求函数
的图象,求函数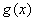 在
在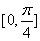 上的最大值和最小值。
上的最大值和最小值。