题目内容
已知函数 ,其图象过点
,其图象过点
(1)求 的值;
的值;
(2)将函数 图象上各点向左平移
图象上各点向左平移 个单位长度,得到函数
个单位长度,得到函数 的图象,求函数
的图象,求函数 在
在 上的单调递增区间.
上的单调递增区间.
【答案】
(1) (2)函数
(2)函数 在
在 上的单调递增区间为
上的单调递增区间为 和
和 .
.
【解析】
试题分析:解:(1)


 ……3分
……3分
又函数图象过点 ,所以
,所以 ,即
,即
又 ,所以
,所以 ……6分
……6分
(2)由(1)知 ,将函数
,将函数 图象上各点向左平移
图象上各点向左平移 个单位长度后,得到函数
个单位长度后,得到函数 的图象,可知
的图象,可知 .……9分
.……9分
因为 ,所以
,所以 ,由
,由 和
和 知函数
知函数 在
在 上的单调递增区间为
上的单调递增区间为 和
和 .……12分
.……12分
考点:三角函数的性质
点评:主要是考查了三角函数的恒等变换,以及三角函数性质的综合运用,属于中档题。

练习册系列答案
相关题目
 ,其图象过点
,其图象过点
 的值;
的值; 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值。
上的最大值和最小值。
 ,其图象过点(
,其图象过点( ,
, ).
). 的值及
的值及 最小正周期;
最小正周期; 的图象,求函数
的图象,求函数 在[0,
在[0,  ]上的最大值和最小值.
]上的最大值和最小值.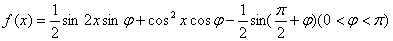 ,其图象过点
,其图象过点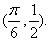
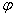 的值;
的值;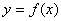 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的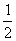 ,纵坐标不变,得到函数
,纵坐标不变,得到函数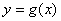 的图象,求函数
的图象,求函数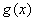 在
在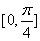 上的最大值和最小值。
上的最大值和最小值。 ,其图象过点(
,其图象过点( ,
, ).
). ]上的最大值和最小值.
]上的最大值和最小值.