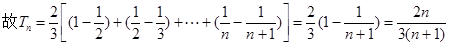题目内容
利用通项求和,求1+11+111+…+
之和.
| ||
| n个1 |
分析:由于
=
×
=
,然后利用分组求和,结合等比数列的求和公式即可求解
| ||
| n个1 |
| 1 |
| 9 |
| ||
| n个 |
| 10n-1 |
| 9 |
解答:解:由于
=
×
=
∴1+11+111+…+
=
[(10-1)+(102-1)+…+(10n-1)]
=
(10+102+…+10n)-
=
•
-
=
| ||
| n个1 |
| 1 |
| 9 |
| ||
| n个 |
| 10n-1 |
| 9 |
∴1+11+111+…+
| ||
| n个1 |
| 1 |
| 9 |
=
| 1 |
| 9 |
| n |
| 9 |
=
| 1 |
| 9 |
| 10(1-10n) |
| 1-10 |
| n |
| 9 |
=
| 10n+1-9n-10 |
| 81 |
点评:本题主要考查了数列的求和及等比数列的求和公式的应用,解题的关键是寻求数列的项的规律

练习册系列答案
相关题目
 的前n项和
的前n项和 满足:
满足: ,
, 和前n项和
和前n项和 的前n项和
的前n项和 ;
; 对任意的
对任意的 ,
, 都成立.
都成立.
 ,然后得到
,然后得到
 得到结论
得到结论 利用裂项求和的思想得到结论。
利用裂项求和的思想得到结论。


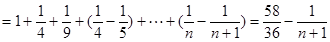
 ∴
∴  ∴
∴
 ∴数列
∴数列 …………………4分
…………………4分 …………………5分
…………………5分  …………………6分
…………………6分
 …………………9分
…………………9分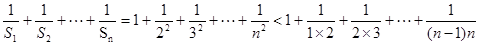
 …………………12分
…………………12分
 之和.
之和.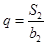 .(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足
.(Ⅰ)求an 与bn;(Ⅱ)设数列{cn}满足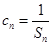 ,求{cn}的前n项和Tn.
,求{cn}的前n项和Tn.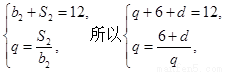 ,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中,
,解得q=3或q=-4(舍),d=3.得到通项公式故an=3+3(n-1)=3n, bn=3 n-1. 第二问中, ,然后利用裂项求和得到Tn.
,然后利用裂项求和得到Tn.