题目内容
下列命题的否定是假命题的个数为
①所有的正方形都是矩形
②所有的一元二次方程都有实数解
③至少存在一个锐角α,使得sinα=![]()
[ ]
A.
3个
B.
2个
C.
1个
D.
0个
答案:B
解析:
解析:
|
先写出各个命题的否定,再根据判断全称命题或存在性命题真假的方法确定其真假.命题①的否定是“存在一个正方形不是矩形”,显然原命题是真命题,其否定是假命题.命题②的否定是“存在一个一元二次方程没有实数解”,显然原命题是假命题,其否定是真命题.命题③的否定是“每一个锐角α都使得sinα= |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
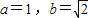 ,
,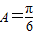 则
则 ;③设二次函数f(x)=x2+ax+a,则“
;③设二次函数f(x)=x2+ax+a,则“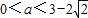 ”是“方程f(x)-x=0的两根x1和x2满足0<x1<x2<1”的充分必要条件.④过点(
”是“方程f(x)-x=0的两根x1和x2满足0<x1<x2<1”的充分必要条件.④过点( ,1)且与函数y=
,1)且与函数y=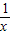 的图象相切的直线方程是4x+y-3=0.其中所有正确说法的序号是 .
的图象相切的直线方程是4x+y-3=0.其中所有正确说法的序号是 .