题目内容
如图，
是边长为1的正三角形，
分别是边
上的点，
段
过的重心
,设
.
（1）当
时，求
的长；
（2）分别记
的面积为
,试将表示为
的函数；
（3）求
的最大值和最小值。
（1）
；
（2）
2分；
（3）
.
解析试题分析：(1)
中，可知
,
是
的重心，所以
,
根据正弦定理：
,可求得的长
(2)
,根据正弦定理，可分别求得
,然后根据
,
;
(3)根据上一问的结果，代入，进行降幂整理，可求得最值.
解：（1）
是边长为1的正三角形，为重心,，
1分
在中 
由正弦定理得 
解得 
3分
（2）在中，
，
由正弦定理得 
在
中，同理可得
2分 2分
(3) = 
2分
当
当 2分
考点：1.重心性质；2.正弦定理；3.面积公式；4.三角函数的化简.
练习册系列答案
相关题目
，且
.
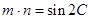，求边c的长．
、
、
、
，欲测量
米，如图，同时也能测量出
，
，
，
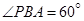，则
.
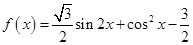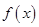的最小正周期及在区间
的最大值；
中，
、
、
所对的边分别是
、
、
，
，
，求
周长
的最大值.
．
，且
，求
的值；
，且△ABC的面积为
，求sinA+sinB的值．
， 
，b＋c＝3，求△ABC的面积．
，sinB＝
cosC．
，求△ABC的面积．
，则sin∠BAC＝________.