题目内容
20.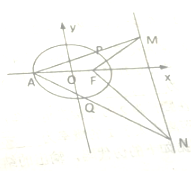 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且离心率e=$\frac{1}{2}$,过椭圆右焦点F作互相垂直的两直线与其右准线交于点M、N,A为椭圆的左顶点,连接AM、AN交椭圆于P,Q两点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点(1,$\frac{3}{2}$),且离心率e=$\frac{1}{2}$,过椭圆右焦点F作互相垂直的两直线与其右准线交于点M、N,A为椭圆的左顶点,连接AM、AN交椭圆于P,Q两点.(1)求椭圆C的方程;
(2)求MN的最小值;
(3)问:直线PQ是否过定点?若过定点,请求出此定点.
分析 (1)由题意的离心率公式和a,b,c的关系,及点满足椭圆方程,解方程可得a,b,进而得到椭圆方程;
(2)求得F(1,0),设出直线FM的方程,代入准线x=4,可得M的坐标,将k换为-$\frac{1}{k}$,可得N的坐标,求得MN的距离,运用基本不等式即可得到所求最小值;
(3)求得A(-2,0),可得AM的方程,代入椭圆方程,运用韦达定理可得P的横坐标,代入直线AM的方程y=$\frac{k}{2}$(x+2),可得P的坐标,将k换为-$\frac{1}{k}$,可得Q的坐标,再由两点的斜率公式计算PQ的斜率,再由点斜式方程可得直线PQ的方程,由直线恒过定点的思想,即可得到定点F(1,0).
解答 解:(1)由题意可得e=$\frac{c}{a}$=$\frac{1}{2}$,a2-b2=c2,
将点(1,$\frac{3}{2}$)代入椭圆方程可得$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,
解方程可得a=2,b=$\sqrt{3}$,c=1,
即有椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)由F(1,0),设FM的方程为y=k(x-1),
联立椭圆的右准线方程x=4,可得M(4,3k),
由FN的方程为y=-$\frac{1}{k}$(x-1),代入x=4,可得N(4,-$\frac{3}{k}$),
可得|MN|=3|k+$\frac{1}{k}$|=3(|k|+$\frac{1}{|k|}$)≥3•2$\sqrt{|k|•\frac{1}{|k|}}$=6,
当且仅当k=±1时,取得|MN|的长取得最小值6;
(3)由A(-2,0),可设直线AM的方程y=$\frac{k}{2}$(x+2),
代入椭圆方程3x2+4y2=12,可得(3+k2)x2+4k2x+4k2-12=0,
由-2•xP=$\frac{4{k}^{2}-12}{3+{k}^{2}}$,即有xP=$\frac{6-2{k}^{2}}{3+{k}^{2}}$,则P的坐标为($\frac{6-2{k}^{2}}{3+{k}^{2}}$,$\frac{6k}{3+{k}^{2}}$),
将k换为-$\frac{1}{k}$,可得Q($\frac{6{k}^{2}-2}{1+3{k}^{2}}$,-$\frac{6k}{1+3{k}^{2}}$),
直线PQ的斜率为kPQ=$\frac{6k(1+3{k}^{2}+3+{k}^{2})}{(6-2{k}^{2})(1+3{k}^{2})-(6{k}^{2}-2)(3+{k}^{2})}$=$\frac{2k}{1-{k}^{2}}$,
直线PQ的方程为y-$\frac{6k}{3+{k}^{2}}$=$\frac{2k}{1-{k}^{2}}$(x-$\frac{6-2{k}^{2}}{3+{k}^{2}}$),
化为y=$\frac{2k}{1-{k}^{2}}$(x-1),显然x=1时,y=0,
则直线PQ恒过定点F(1,0).
点评 本题考查椭圆方程的求法,注意运用离心率和点满足椭圆方程,考查两点的距离的最值,注意运用基本不等式,同时考查直线恒过定点的求法,注意运用直线方程和椭圆方程联立,求交点,运用直线的点斜式方程,考查化简整理的运算能力,属于中档题.

| A. | 2 | B. | 3 | C. | 11 | D. | 18 |
| A. | ($\frac{π}{2}$,$\frac{3π}{2}$) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (-$\frac{π}{2}$,$\frac{π}{2}$) | D. | (-$\frac{π}{4}$,$\frac{π}{4}$) |