题目内容
定义在R上的可导函数
，在闭区间
上有最大值15，最小值-1，则
的取值范围是（ ）
A． | B． | C． | D． |
D
解析试题分析：对
求导可得
令
，可得
所以
，根据二次函数的图象和性质，可知
所以的取值范围是.
考点：本小题主要考查函数的求导、二次函数的图象和性质，考查学生的转化能力和计算求解能力以及数形结合思想方法的应用.
点评：求出
后，函数化为二次函数，解决二次函数的最值问题，一定要画出二次函数的图象，结合函数的图象进行求解.
练习册系列答案
相关题目
已知函数
，则函数y=f(x)-log3x在（-1，3］上的零点的个数为
| A．4 | B．3 | C．2 | D．1 |
已知函数
的定义域和值域都是[0，1]，则a=（ ）
A． | B． | C． | D．2 |
若
（其中
），则函数
的图象( ）
| A．关于y轴对称 | B．关于X轴对称 |
| C．关于直线y=x轴称 | D．关于原点对称 |
已知幂函数
是定义在区间
上的奇函数，则
（ ）
| A．8 | B．4 | C．2 | D．1 |
若
，则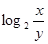
的值为（ ）
| A．0 | B．2 | C．－2 | D．0或2 |
若定义运算
，则函数
的最小值（ ）
| A．0 | B．1 | C．-1 | D．不存在 |
的图象只可能是 （ ）
设
，则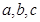
的大小关系是 （ ）
A． | B． |
C． | D． . |