题目内容
已知
,
,
为两两垂直的单位向量,非零向量
=a1
+a2
+a3
(a1,a2,a3∈R),若向量
与向量
,
,
的夹角分别为α,β,γ,则cos2α+cos2β+cos2γ=
| i |
| j |
| k |
| a |
| i |
| j |
| k |
| a |
| i |
| j |
| k |
1
1
.分析:由题意可得,
•
=
•
=
•
=0且|
|=|
|=|
|=1,代入向量的夹角公式可求cosα=
=
,同理可求,cosβ,cosγ,代入即可求解
| i |
| j |
| i |
| k |
| j |
| k |
| i |
| j |
| k |
| ||||
|
|
| a1 | ||
|
解答:解:由题意可得,
•
=
•
=
•
=0且|
|=|
|=|
|=1
∵
=a1
+a2
+a3
∴
•
=a1,
•
=a2,
•
=a3,|
|=
∴cosα=
=
同理可得,cosβ=
cosγ=
∴cos2α+cos2β+cos2γ=1
故答案为:1
| i |
| j |
| i |
| k |
| j |
| k |
| i |
| j |
| k |
∵
| a |
| i |
| j |
| k |
∴
| a |
| i |
| a |
| j |
| a |
| k |
| a |
(a1
|
∴cosα=
| ||||
|
|
| a1 | ||
|
同理可得,cosβ=
| a2 | ||
|
cosγ=
| a3 | ||
|
∴cos2α+cos2β+cos2γ=1
故答案为:1
点评:本题主要考查了向量的数量积的运算,向量的夹角公式的应用,属于公式的简单应用

练习册系列答案
相关题目
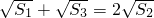 ,求S5;
,求S5;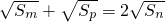 ,求数列的通项an;
,求数列的通项an;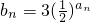 (n∈N*),集合Tn={bi•bj|1≤i≤j≤n,i,j∈N*},记集合Tn中所有元素之和Bn,试问:是否存在正整数n和正整数k,使得不等式
(n∈N*),集合Tn={bi•bj|1≤i≤j≤n,i,j∈N*},记集合Tn中所有元素之和Bn,试问:是否存在正整数n和正整数k,使得不等式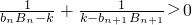 成立?若存在,请求出所有n和k的值;若不存在,请说明理由.
成立?若存在,请求出所有n和k的值;若不存在,请说明理由.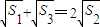 ,求S5;
,求S5;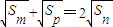 ,求数列的通项an;
,求数列的通项an;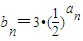 (n∈N*),集合Tn={bi•bj|1≤i≤j≤n,i,j∈N*},记集合Tn中所有元素之和Bn,试问:是否存在正整数n和正整数k,使得不等式
(n∈N*),集合Tn={bi•bj|1≤i≤j≤n,i,j∈N*},记集合Tn中所有元素之和Bn,试问:是否存在正整数n和正整数k,使得不等式 成立?若存在,请求出所有n和k的值;若不存在,请说明理由.
成立?若存在,请求出所有n和k的值;若不存在,请说明理由.