题目内容
已知等差数列{an}的各项均为正数,其前n项和为Sn,首项a1=1.
(Ⅰ)若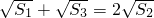 ,求S5;
,求S5;
(Ⅱ)若数列{an}中存在两两互异的正整数m、n、p同时满足下列两个条件:①m+p=2n;②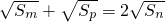 ,求数列的通项an;
,求数列的通项an;
(Ⅲ)对于(Ⅱ)中的数列{an},设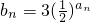 (n∈N*),集合Tn={bi•bj|1≤i≤j≤n,i,j∈N*},记集合Tn中所有元素之和Bn,试问:是否存在正整数n和正整数k,使得不等式
(n∈N*),集合Tn={bi•bj|1≤i≤j≤n,i,j∈N*},记集合Tn中所有元素之和Bn,试问:是否存在正整数n和正整数k,使得不等式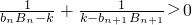 成立?若存在,请求出所有n和k的值;若不存在,请说明理由.
成立?若存在,请求出所有n和k的值;若不存在,请说明理由.
解:(Ⅰ)∵等差数列,∴S3=a1+a2+a3=3a2,
又∵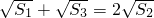 ,∴
,∴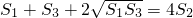 ,
,
∵S1=a1=1,∴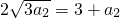 ,
,
∴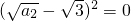 ,
,
∴a2=3,则公差d=2,S5=25.
(Ⅱ)∵等差数列{an},∴设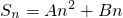 ,
,
∵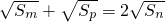 ,
,
∴ ,
,
即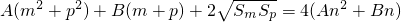 =A(m+p)2+2B(m+p),
=A(m+p)2+2B(m+p),
∴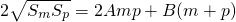 ,
,
两边平方得,4(Am2+Bm)(Ap2+Bp)=4A2m2p2+4ABmp(m+p)+B2(m+p)2,
∴4B2mp=B2(m+p)2,
即B2(m-p)2=0,∵m≠p,∴B=0,又a1=S1=1,∴A=1.
当n≥2时,an=Sn-Sn-1=2n-1,a1=1适合,∴an=2n-1.
(Ⅲ)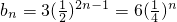 ,
,
则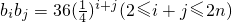 ,
,
∴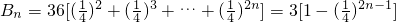 .
.
∵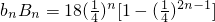 ,
,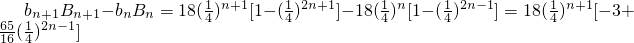 ,
,
∵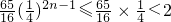 ,
,
∴bn+1Bn+1-bnBn<0,∴数列{bnBn}是递减数列,
由已知不等式得,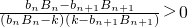 ,∵bn+1Bn+1-bnBn<0,
,∵bn+1Bn+1-bnBn<0,
∴bn+1Bn+1<k<bnBn.
又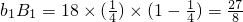 ,
,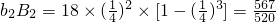 ,
,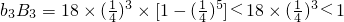 ,∴当n≥3时,bnBn<1,
,∴当n≥3时,bnBn<1,
∴当n=1时,k=2或3;当n=2时,k=1,
故存在正整数n、k使不等式成立,所有n和k的值为:n=1,k=2或3;n=2,k=1.
分析:(Ⅰ)由等差数列性质,知S3=a1+a2+a3=3a2,由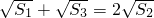 和首项a1=1,得
和首项a1=1,得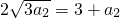 ,由此能求出S5.
,由此能求出S5.
(Ⅱ)设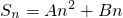 ,由
,由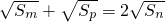 ,导出
,导出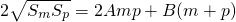 ,由此入手,能够求出an.
,由此入手,能够求出an.
(Ⅲ)由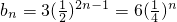 ,知
,知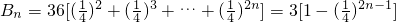 .由此入手,能够推导出存在正整数n、k使不等式成立,并能求出所有n和k的值.
.由此入手,能够推导出存在正整数n、k使不等式成立,并能求出所有n和k的值.
点评:本题考查数列的前n项和、数列的通项公式的求法.综合性强,难度大,有一定的探索性.解题时要认真审题,仔细解答,注意合理地进行等价转化.
又∵
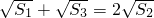 ,∴
,∴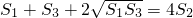 ,
,∵S1=a1=1,∴
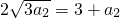 ,
,∴
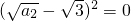 ,
,∴a2=3,则公差d=2,S5=25.
(Ⅱ)∵等差数列{an},∴设
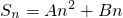 ,
,∵
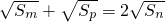 ,
,∴
 ,
,即
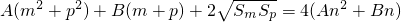 =A(m+p)2+2B(m+p),
=A(m+p)2+2B(m+p),∴
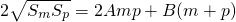 ,
,两边平方得,4(Am2+Bm)(Ap2+Bp)=4A2m2p2+4ABmp(m+p)+B2(m+p)2,
∴4B2mp=B2(m+p)2,
即B2(m-p)2=0,∵m≠p,∴B=0,又a1=S1=1,∴A=1.
当n≥2时,an=Sn-Sn-1=2n-1,a1=1适合,∴an=2n-1.
(Ⅲ)
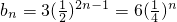 ,
,则
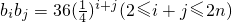 ,
,∴
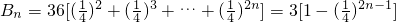 .
.∵
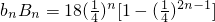 ,
,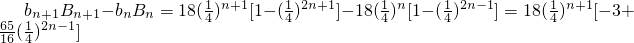 ,
,∵
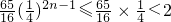 ,
,∴bn+1Bn+1-bnBn<0,∴数列{bnBn}是递减数列,
由已知不等式得,
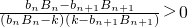 ,∵bn+1Bn+1-bnBn<0,
,∵bn+1Bn+1-bnBn<0,∴bn+1Bn+1<k<bnBn.
又
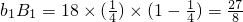 ,
,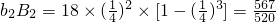 ,
,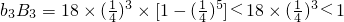 ,∴当n≥3时,bnBn<1,
,∴当n≥3时,bnBn<1,∴当n=1时,k=2或3;当n=2时,k=1,
故存在正整数n、k使不等式成立,所有n和k的值为:n=1,k=2或3;n=2,k=1.
分析:(Ⅰ)由等差数列性质,知S3=a1+a2+a3=3a2,由
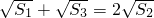 和首项a1=1,得
和首项a1=1,得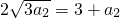 ,由此能求出S5.
,由此能求出S5.(Ⅱ)设
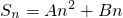 ,由
,由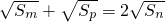 ,导出
,导出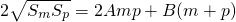 ,由此入手,能够求出an.
,由此入手,能够求出an.(Ⅲ)由
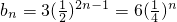 ,知
,知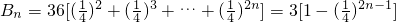 .由此入手,能够推导出存在正整数n、k使不等式成立,并能求出所有n和k的值.
.由此入手,能够推导出存在正整数n、k使不等式成立,并能求出所有n和k的值.点评:本题考查数列的前n项和、数列的通项公式的求法.综合性强,难度大,有一定的探索性.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.