题目内容
数列{an}是递增的等差数列,且a1+a6=﹣6,a3•a4=8.
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn的最小值;
(3)求数列{|an|}的前n项和Tn.
【解析】(1)由 得:
得: ,
,
∴a3、a4是方程x2+6x+8=0的二个根,
∴x1=﹣2,x2=﹣4;
∵等差数列{an}是递增数列,
∴a3=﹣4,a4=﹣2,
∴公差d=2,a1=﹣8.
∴an=2n﹣10;
(2)∵Sn= =n2﹣9n=
=n2﹣9n= ﹣
﹣ ,
,
∴(Sn)min=S4=S5=﹣20;
(3)由an≥0得2n﹣10≥0,解得n≥5,此数列前四项为负的,第五项为0,从第六项开始为正的.
当1≤n≤5且n∈N*时,
Tn=|a1|+|a2|+…+|an|
=﹣(a1+a2+…+an)
=﹣Sn
=﹣n2+9n;
当n≥6且n∈N*时,
Tn=|a1|+|a2|+…+|a5|+|a6|+…+|an|
=﹣(a1+a2+…+a5)+(a6+…+an)
=Sn﹣2S5
=n2﹣9n﹣2(25﹣45)
=n2﹣9n+40.
∴Tn= .
.

练习册系列答案
相关题目
 的一般方程为
的一般方程为 ,则下列说法中不正确的是( )
,则下列说法中不正确的是( ) .圆
.圆
 .圆
.圆 轴截得的弦长为
轴截得的弦长为
 .圆
.圆
 .圆
.圆 轴截得的弦长为
轴截得的弦长为
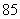 、
、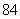 B.
B. 、
、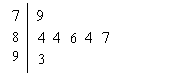
 ,若z的最小值为3,则m的值为( )
,若z的最小值为3,则m的值为( )
 的函数
的函数 满足
满足 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数的取值范围为( )
恒成立,则实数的取值范围为( ) 的图象大致为 ( )
的图象大致为 ( )
 ,则复数
,则复数 在复平面上对应的点位于
在复平面上对应的点位于