题目内容
(本题满分为12分)
如图所示:已知 ⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作
⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作 于E,求证:
于E,求证: .
.

【答案】
证明:PA 面ABC
面ABC PA
PA  BC
BC


 面ACP
面ACP




 面PBC
面PBC
【解析】
试题分析:由PA 面ABC,BC
面ABC,BC 面ABC,所以PA
面ABC,所以PA  BC,又因为
BC,又因为 ,
, ,所以
,所以 面ACP
面ACP
所以  ,又因为
,又因为 ,
,
 ,所以
,所以 面PBC。
面PBC。
考点:线面垂直的判定和性质
点评:线面垂直的判定定理中面内两直线要相交

练习册系列答案
相关题目
 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
. 的值;
的值; 在区间
在区间 上的最大值;
上的最大值; ,曲线
,曲线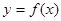 上是否存在两点
上是否存在两点 ,使得
,使得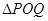 是以
是以 .
. 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程. 的图像过坐标原点
的图像过坐标原点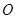 ,且在点
,且在点 处的切线
处的切线 .
. 的值; (2)求
的值; (2)求 在区间
在区间 上的最大值;
上的最大值;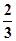 .
.
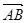 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.