题目内容
(本题满分为12分)已知椭圆中心在原点,焦点在y轴上,焦距为4,离心率为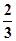 .
.

(I)求椭圆方程;
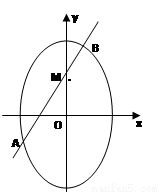
(II)设椭圆在y轴的正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段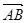 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
【答案】
(I)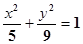 . (II)
. (II)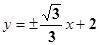 .
.
【解析】(I)根据题意知c=2,a=3,所以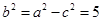 ,所以椭圆方程为
,所以椭圆方程为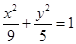 .
.
(II) 设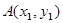 ,
,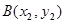 ,过A,B的直线方程为
,过A,B的直线方程为 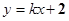 由M分有向线段
由M分有向线段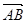 所
所
成的比为2,得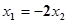 (*),再由
(*),再由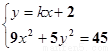 得
得 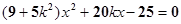 ,
,
根据韦达定理再得到两个关于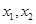 的方程,再与(*)方程结合解方程组可解出k值.
的方程,再与(*)方程结合解方程组可解出k值.
解:(I)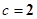 ,
,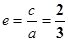 ,
,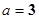 ,
,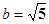 .
.
所以,所求椭圆方程为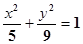 . (5分)
. (5分)
(II)设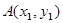 ,
,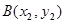 ,
,
过A,B的直线方程为 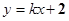 由M分有向线段
由M分有向线段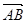 所
所
成的比为2,得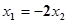 ,(6分)
,(6分)
则由 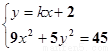 得
得 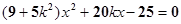 (8分)
(8分)
故 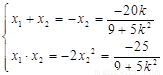 , 消 x2得
, 消 x2得 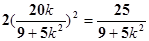
解得 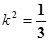 ,
,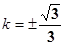 (11分)所以,
(11分)所以,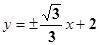 . (12分)
. (12分)

练习册系列答案
相关题目
 ⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作
⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A作 于E,求证:
于E,求证: .
. 
 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点 处的切线的斜率是
处的切线的斜率是 .
. 的值;
的值; 在区间
在区间 上的最大值;
上的最大值; ,曲线
,曲线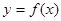 上是否存在两点
上是否存在两点 ,使得
,使得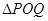 是以
是以 .
. 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程. 的图像过坐标原点
的图像过坐标原点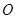 ,且在点
,且在点 处的切线
处的切线 .
. 的值; (2)求
的值; (2)求 在区间
在区间 上的最大值;
上的最大值;