题目内容
把函数y=cosx- sinx的图象沿向量
sinx的图象沿向量 =(-m,m)(m>0)的方向平移后,所得的图象关于y轴对称,则m的最小值是( )
=(-m,m)(m>0)的方向平移后,所得的图象关于y轴对称,则m的最小值是( )A.

B.

C.

D.

【答案】分析:函数y=-2sin(x-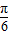 ),平移后,所得的函数为 y=-2sin(x+m-
),平移后,所得的函数为 y=-2sin(x+m-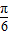 )+m,可得 y=-2sin(x+m-
)+m,可得 y=-2sin(x+m-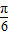 )+m 是偶函数,m-
)+m 是偶函数,m-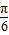 =kπ+
=kπ+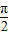 ,k∈z,从而得到正数m的最小值.
,k∈z,从而得到正数m的最小值.
解答:解:函数y=cosx-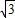 sinx=2sin(
sinx=2sin(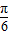 -x)=-2sin(x-
-x)=-2sin(x-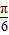 ),将此函数的图象按向量a=(-m,m)(m>0)的方向平移后,所得的函数为 y=-2sin(x+m-
),将此函数的图象按向量a=(-m,m)(m>0)的方向平移后,所得的函数为 y=-2sin(x+m-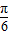 )+m,所得的图象关于y轴对称,故 y=-2sin(x+m-
)+m,所得的图象关于y轴对称,故 y=-2sin(x+m-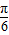 )+m 是偶函数,
)+m 是偶函数,
∴m-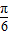 =kπ+
=kπ+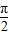 ,k∈z,即 m=kπ+
,k∈z,即 m=kπ+ π,故正数m的最小值是
π,故正数m的最小值是 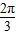 ,
,
故选 C.
点评:本题考查函数y=Asin(ωx+∅)的图象变换,偶函数的图象特征,得到 m-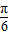 =kπ+
=kπ+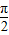 ,k∈z,是解题的关键.
,k∈z,是解题的关键.
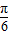 ),平移后,所得的函数为 y=-2sin(x+m-
),平移后,所得的函数为 y=-2sin(x+m-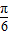 )+m,可得 y=-2sin(x+m-
)+m,可得 y=-2sin(x+m-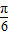 )+m 是偶函数,m-
)+m 是偶函数,m-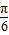 =kπ+
=kπ+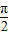 ,k∈z,从而得到正数m的最小值.
,k∈z,从而得到正数m的最小值.解答:解:函数y=cosx-
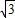 sinx=2sin(
sinx=2sin(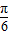 -x)=-2sin(x-
-x)=-2sin(x-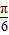 ),将此函数的图象按向量a=(-m,m)(m>0)的方向平移后,所得的函数为 y=-2sin(x+m-
),将此函数的图象按向量a=(-m,m)(m>0)的方向平移后,所得的函数为 y=-2sin(x+m-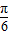 )+m,所得的图象关于y轴对称,故 y=-2sin(x+m-
)+m,所得的图象关于y轴对称,故 y=-2sin(x+m-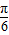 )+m 是偶函数,
)+m 是偶函数,∴m-
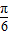 =kπ+
=kπ+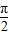 ,k∈z,即 m=kπ+
,k∈z,即 m=kπ+ π,故正数m的最小值是
π,故正数m的最小值是 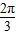 ,
,故选 C.
点评:本题考查函数y=Asin(ωx+∅)的图象变换,偶函数的图象特征,得到 m-
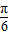 =kπ+
=kπ+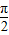 ,k∈z,是解题的关键.
,k∈z,是解题的关键. 
练习册系列答案
相关题目
把函数y=cosx-
sinx的图象沿向量
=(-m,m)(m>0)的方向平移后,所得的图象关于y轴对称,则m的最小值是( )
| 3 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
把函数y=cosx的图象按向量
=(-
,-2)平移后得到的图象的解析式是( )
| a |
| π |
| 3 |
A、y=cos(x-
| ||
B、y=cos(x+
| ||
C、y=cos(x-
| ||
D、y=cos(x+
|
把函数y=cosx的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),然后把图象向左平移
个单位,则所得图形对应的函数解析式为( )
| π |
| 4 |
A、y=cos(
| ||||
B、y=cos(2x+
| ||||
C、y=cos(
| ||||
| D、y=-sin2x |