题目内容
函数y=2x2-lnx的单调增区间为______.
函数y=2x2-lnx的定义域为(0,+∞)
对函数y=2x2-lnx求导,得,y′=4x-
,
令y′>0,即4x-
>0,解得,x>
∴函数的单调增区间为(
,+∞)
故答案为(
,+∞)
对函数y=2x2-lnx求导,得,y′=4x-
| 1 |
| x |
令y′>0,即4x-
| 1 |
| x |
| 1 |
| 2 |
∴函数的单调增区间为(
| 1 |
| 2 |
故答案为(
| 1 |
| 2 |

练习册系列答案
相关题目
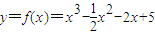 ;
; ;
;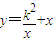 (k>0);
(k>0);