题目内容
已知A(1,f'(1))是函数y=f(x)的导函数图象上的一点,点B为(x,ln(x+1)),向量
=(1,1),令f(x)=
•
.
(1)求函数y=f(x)的表达式;
(2)若x>0,证明:f(x)>
;
(3)若x∈[-1,1]时,不等式
x2≤f(x2)+m2-
m-3都恒成立,求实数m的取值范围.
| a |
| AB |
| a |
(1)求函数y=f(x)的表达式;
(2)若x>0,证明:f(x)>
| 2x2+3x-10 |
| 2(x+2) |
(3)若x∈[-1,1]时,不等式
| 1 |
| 2 |
| 9 |
| 2 |
(1)∵A(1,f'(1)),B(x,ln(x+1)),∴
=(x-1,ln(x+1)-f′(1))
∴f(x)=ln(x+1)+x-f'(1)-1,∴f′(x)=
+1,∴f′(1)=
∴f(x)=ln(x+1)+x-
(2)设g(x)=f(x)-
=ln(x+1)-
∴g′(x)=
-
=
>0
在(0,+∞)上是增函数,又∵g(0)=0∴g(x)>0,∴f(x)>
(3)由
x2≤f(x2)+m2-
m-3得m2-
m-
≥-ln(x2+1)-
设h(x)=-ln(x2+1)-
,∴h′(x)=-
∴当x∈[-1,0]时,h'(x)>0,h(x)为递增;
当x∈[0,1]时,h'(x)<0,h(x)为递减
∴h(x)max=h(0)=0,∴m2-
m-
≥0,解得m≤-1或m≥
∴实数m的取值范围是m≤-1或m≥
| AB |
∴f(x)=ln(x+1)+x-f'(1)-1,∴f′(x)=
| 1 |
| x+1 |
| 3 |
| 2 |
| 5 |
| 2 |
(2)设g(x)=f(x)-
| 2x2+3x-10 |
| 2(x+2) |
| 2x |
| x+2 |
| 1 |
| x+1 |
| 4 |
| (x+2)2 |
| x2 |
| (x+1)(x+2)2 |
在(0,+∞)上是增函数,又∵g(0)=0∴g(x)>0,∴f(x)>
| 2x2+3x-10 |
| 2(x+2) |
(3)由
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 11 |
| 2 |
| x2 |
| 2 |
设h(x)=-ln(x2+1)-
| x2 |
| 2 |
| x(x2+3) |
| x2+1 |
当x∈[0,1]时,h'(x)<0,h(x)为递减
∴h(x)max=h(0)=0,∴m2-
| 9 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
∴实数m的取值范围是m≤-1或m≥
| 11 |
| 2 |

练习册系列答案
相关题目
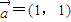 ,令
,令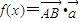 .
. ;
;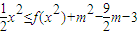 都恒成立,求实数m的取值范围.
都恒成立,求实数m的取值范围.