题目内容
求下列函数单调区间:(1)y=f(x)=x3-
| 1 |
| 2 |
(2)y=
| x2-1 |
| x |
(3)y=
| k2 |
| x |
(4)y=2x2-lnα.
分析:首先求出函数的导数,然后令f′(x)=0,解出函数的极值点,最好根据导数与函数单调性的关系进行求解.
解答:解:(1)由题意得f′(x)=3x2-x-2,
令f′(x)=0,解得x=1或-
,
当x<-
或x>1时,f′(x)>0,
∴(-∞,-
)∪(1,+∞)为f(x)的单调递增区间,
当-
≤x≤1时,f′(x)<0,
∴[-
,1]为f(x)的单调递减区间.
(2)∵y=
,
∴y′=
>0,
∴y在(-∞,+∞)上是增函数;
∴y的单调增区间为(-∞,+∞);
(3)∵y=
+x(k>0),
∴y′=
+1=
令y′=0得,x2-k2=0,
解得x=±k,
∴当y′>0时,即y在(k,+∞)∪(-∞,-k)上为增函数;
当y′<0时,即y在[-k,k]上为减函数;
(4)∵y=2x2-lnα,
∴y′=4x,
令y′=0,解得x=0,
∴当x>0时,y′>0,y为增函数;
当x<0时,y′<0,y为减函数;
∴y的增区间为(0,+∞),减区间为(-∞,0);
令f′(x)=0,解得x=1或-
| 2 |
| 3 |
当x<-
| 2 |
| 3 |
∴(-∞,-
| 2 |
| 3 |
当-
| 2 |
| 3 |
∴[-
| 2 |
| 3 |
(2)∵y=
| x2-1 |
| x |
∴y′=
| x2+1 |
| x2 |
∴y在(-∞,+∞)上是增函数;
∴y的单调增区间为(-∞,+∞);
(3)∵y=
| k2 |
| x |
∴y′=
| -k2 |
| x2 |
| x2-k2 |
| x2 |
令y′=0得,x2-k2=0,
解得x=±k,
∴当y′>0时,即y在(k,+∞)∪(-∞,-k)上为增函数;
当y′<0时,即y在[-k,k]上为减函数;
(4)∵y=2x2-lnα,
∴y′=4x,
令y′=0,解得x=0,
∴当x>0时,y′>0,y为增函数;
当x<0时,y′<0,y为减函数;
∴y的增区间为(0,+∞),减区间为(-∞,0);
点评:此题主要考查函数导数与函数单调性之间的关系,需要掌握并会熟练运用导数判断函数的单调性.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
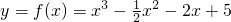 .
.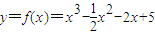 ;
; ;
;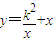 (k>0);
(k>0);