题目内容
已知函数 (常数
(常数 )在
)在 处取得极大值M.
处取得极大值M.
(Ⅰ)当M= 时,求
时,求 的值;
的值;
(Ⅱ)记 在
在 上的最小值为N,若
上的最小值为N,若 ,求
,求 的取值范围.
的取值范围.
(1)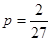 (2)
(2)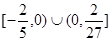
解析试题分析:解(Ⅰ) ,由于函数
,由于函数 (常数
(常数 )在
)在 处取得极大值M
处取得极大值M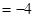 ,故有
,故有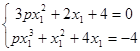
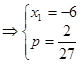 (
(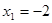 时,
时,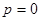 不合题意,舍去),当
不合题意,舍去),当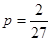 时,经检验,函数
时,经检验,函数 在
在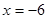 处取得极大值(在
处取得极大值(在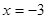 处取得极小值),故所求
处取得极小值),故所求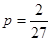
(Ⅱ)当 时,由
时,由 ,即
,即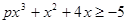 成立,得
成立,得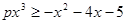 (1)
(1)
当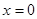 时,不等式(1)成立
时,不等式(1)成立
当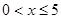 ,不等式(1)可化为
,不等式(1)可化为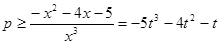 (这里
(这里 ),令
),令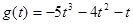 ,则
,则 ,所以
,所以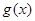 在
在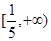 单调递减,故
单调递减,故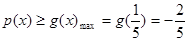
当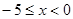 ,不等式(1)可化为
,不等式(1)可化为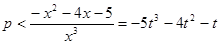 (这里
(这里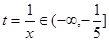 ),设
),设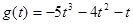 ,
,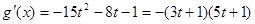
由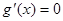 ,得到
,得到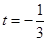 或
或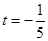 ,讨论可知:
,讨论可知: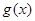 在
在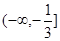 单调递减,在
单调递减,在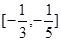 单调递增,故
单调递增,故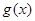 在
在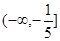 的最小值是
的最小值是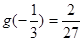 ,故
,故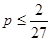
综合上述(1)(2)(3)可得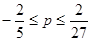 ,又因为
,又因为 ,故所求
,故所求 的取值范围是
的取值范围是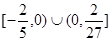
考点:导数的运用
点评:解决的关键是利用导数的几何意义,以及导数的符号来判定函数单调性,进而求解最值,属于基础题。

练习册系列答案
相关题目
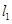 与直线4x-y-1=0平行,且点 P0 在第三象限,
与直线4x-y-1=0平行,且点 P0 在第三象限,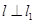 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.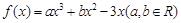 ,且
,且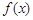 在
在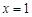 和
和 处取得极值.
处取得极值. ,是否存在实数
,是否存在实数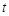 ,使得曲线
,使得曲线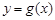 与
与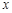 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出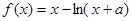 的最小值为0,其中
的最小值为0,其中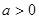 。
。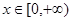 ,有
,有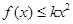 成立,求实数k的最小值
成立,求实数k的最小值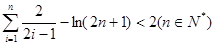
 .
. 的单调区间与极值;
的单调区间与极值; ,使得对任意的
,使得对任意的 ,当
,当 时恒有
时恒有 成立.若存在,求
成立.若存在,求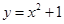 ,直线
,直线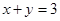 以及两坐标轴所围成的图形的面积S.
以及两坐标轴所围成的图形的面积S.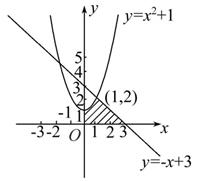
 ,其中
,其中 .
. 有极值,求
有极值,求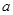 的取值范围;
的取值范围; ,
, 恒成立,求
恒成立,求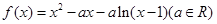
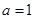 时,求函数
时,求函数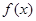 的最值;
的最值;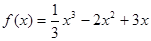 (
(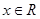 )的图象为曲线
)的图象为曲线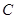 .
.