题目内容
11．若圆锥的底面半径长为4，高为6，在这个圆锥内有一个内接圆柱，设这个圆柱的高为x，则当x取何值时，圆柱的侧面积最大（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 设圆柱的底面半径为r，由由△PDN∽△PAO，得$\frac{DN}{AO}$=$\frac{PN}{PO}$，从而求出r=$\frac{12-2x}{3}$，进而得到圆柱的侧面积S=2πr•x=-$\frac{4π}{3}$（x-3）2+12π，（0＜x＜6）．由此能求出结果．
解答 解：如图，设圆柱的底面半径为r，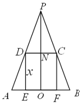
则由△PDN∽△PAO，得$\frac{DN}{AO}$=$\frac{PN}{PO}$
即$\frac{r}{4}=\frac{6-x}{6}$，解得r=$\frac{12-2x}{3}$，
∴圆柱的侧面积S=2πr•x=-$\frac{4}{3}π{x}^{2}$+8πx=-$\frac{4π}{3}$（x-3）2+12π，（0＜x＜6）．
∴当x=3时，圆柱的侧面积取最大值Smax=12π．…（12分）
故选：B．
点评 本题考查圆柱的侧面积的最大值的求法，是中档题，解题时要认真审题，注意圆锥、圆柱的性质的合理运用．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，右焦点为F，过点F的直线交椭圆于A，B两点，当A为下顶点时，|AF|=2．
6．等差数列{an}中，a2+a4=2，a3+a5=8，那么它的公差是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
16．已知向量$\overrightarrow a=（1，2）$，点A（-1，1），B（2，y），若向量$\overrightarrow{AB}$∥$\overrightarrow a$，则实数y的值为（ ）
| A． | 5 | B． | 7 | C． | 6 | D． | 8 |
20．已知直线a，b分别在两个不同的平面α，β内．则“直线a和直线b没有公共点”是“平面α和平面β平行”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
如图所示，已知正六边形ABCDEF的边长为2，O为它的中心，将它沿对角线FC折叠，使平面ABCF⊥平面FCDE，点G是边AB的中点．