题目内容
已知命题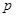 :方程
:方程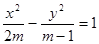 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆;
命题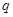 :双曲线
:双曲线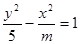 的离心率
的离心率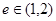 ,若
,若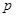 或
或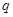 为真命题,
为真命题,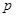 且
且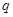 为假命题,求实数
为假命题,求实数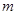 的取值范围.
的取值范围.
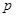 :方程
:方程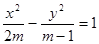 表示焦点在y轴上的椭圆;
表示焦点在y轴上的椭圆;命题
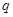 :双曲线
:双曲线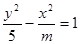 的离心率
的离心率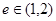 ,若
,若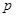 或
或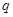 为真命题,
为真命题,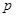 且
且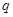 为假命题,求实数
为假命题,求实数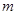 的取值范围.
的取值范围. <15
<15试题分析:研究四种命题关系,首先研究各命题为真时的充要条件,命题
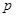 为真命题,则
为真命题,则
所以
 ,命题q为真命题,则
,命题q为真命题,则 且
且 ,所以
,所以 ;其次研究复合命题真假性,确定简单命题真假性,因为p或q为真,p且q为假,所以p与q为一真一假,对于命题为假的情形,取命题为真时范围的补集,本题分两组求解,取其并集.
;其次研究复合命题真假性,确定简单命题真假性,因为p或q为真,p且q为假,所以p与q为一真一假,对于命题为假的情形,取命题为真时范围的补集,本题分两组求解,取其并集.  或
或 ,因此m的取值范围为
,因此m的取值范围为 <15
<15试题解析:解:若p为真命题则

所以
 ; 2分
; 2分若q为真命题则
 且
且
所以
 4分
4分(1)若
 则 无解 8分
则 无解 8分(2)若
 则
则  <15
<15故m的取值范围为
 <15 12分
<15 12分
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 +y2=1上的三个点,O是坐标原点.
+y2=1上的三个点,O是坐标原点. ,且过点M
,且过点M 。
。 的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。
的直线l交椭圆C于A、B两点,且N恰好为AB中点,能否在椭圆C上找到点D,使△ABD的面积最大?若能,求出点D的坐标;若不能,请说明理由。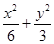 =1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
=1,A1,A2分别为椭圆C1的左、右顶点.椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”.
 轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1 F2B2是一个面积为8的正方形.
 +
+ =1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
=1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 . +y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.
+y2=1,在椭圆C上任取不同两点A,B,点A关于x轴的对称点为A′,当A,B变化时,如果直线AB经过x轴上的定点T(1,0),则直线A′B经过x轴上的定点为________.

 的两焦点,过点F2的直线交椭圆于A,B两点.在
的两焦点,过点F2的直线交椭圆于A,B两点.在