题目内容
已知函数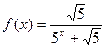 ,
,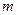 为正整数.
为正整数.
(Ⅰ)求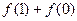 和
和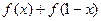 的值;
的值;
(Ⅱ)数列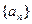 的通项公式为
的通项公式为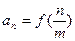 (
(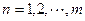 ),求数列
),求数列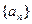 的前
的前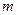 项和
项和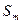 ;
;
(Ⅲ) (4分)设数列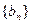 满足:
满足: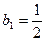 ,
,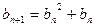 ,设
,设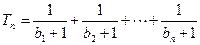 ,若(Ⅱ)中的
,若(Ⅱ)中的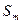 满足:对任意不小于3的正整数n,
满足:对任意不小于3的正整数n,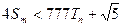 恒成立,试求m的最大值.
恒成立,试求m的最大值.
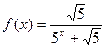 ,
,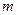 为正整数.
为正整数.(Ⅰ)求
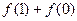 和
和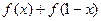 的值;
的值; (Ⅱ)数列
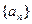 的通项公式为
的通项公式为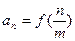 (
(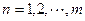 ),求数列
),求数列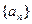 的前
的前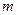 项和
项和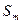 ;
;(Ⅲ) (4分)设数列
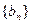 满足:
满足: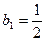 ,
,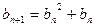 ,设
,设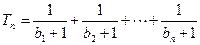 ,若(Ⅱ)中的
,若(Ⅱ)中的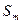 满足:对任意不小于3的正整数n,
满足:对任意不小于3的正整数n,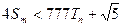 恒成立,试求m的最大值.
恒成立,试求m的最大值.解:(Ⅰ)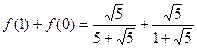 ="1;"
="1;"
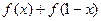 =
=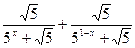 =
=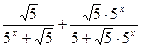 ="1; "
="1; "
(Ⅱ)由(Ⅰ)得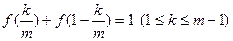 ,
,
即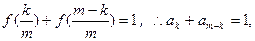
由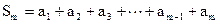 , ①
, ①
得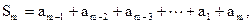 ②
②
由①+②, 得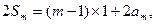
∴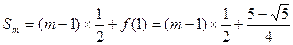 ,
,
(Ⅲ) 解:∵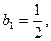
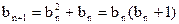 ,∴对任意的
,∴对任意的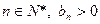 .
.
∴ 即
即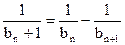 .
.
∴ .
.
∵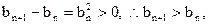 ∴数列
∴数列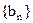 是单调递增数列.
是单调递增数列.
∴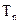 关于n递增. 当
关于n递增. 当 , 且
, 且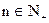 时,
时, 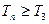 .
.
∵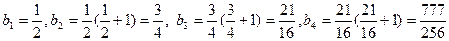

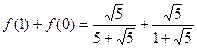 ="1;"
="1;" 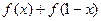 =
=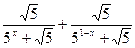 =
=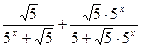 ="1; "
="1; " (Ⅱ)由(Ⅰ)得
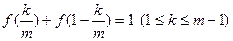 ,
,即
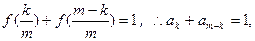
由
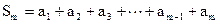 , ①
, ① 得
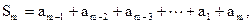 ②
② 由①+②, 得
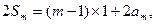
∴
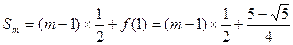 ,
, (Ⅲ) 解:∵
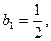
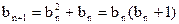 ,∴对任意的
,∴对任意的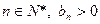 .
. ∴
 即
即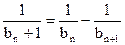 .
. ∴
 .
. ∵
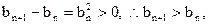 ∴数列
∴数列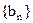 是单调递增数列.
是单调递增数列. ∴
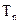 关于n递增. 当
关于n递增. 当 , 且
, 且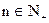 时,
时, 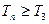 .
. ∵
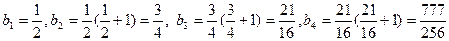

略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
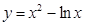 上的一个动点,则点P到直线
上的一个动点,则点P到直线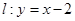 的距离的最小值为( )
的距离的最小值为( )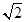
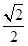
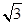
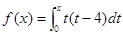 在
在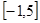 上( )
上( )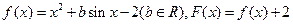 ,且对于任意实数
,且对于任意实数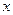 ,恒有
,恒有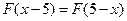 。
。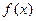 的解析式;
的解析式;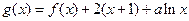 在区间
在区间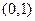 上单调,求实数
上单调,求实数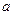 的取值范围;
的取值范围;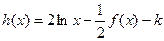 有几个零点?
有几个零点?
 的单调性;
的单调性; 的最大值和最小值.
的最大值和最小值. ,已知
,已知 在
在 时取得极值,则
时取得极值,则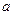 =( )
=( )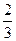 ,那么这个三角形顶角的正弦值 ( )
,那么这个三角形顶角的正弦值 ( ) 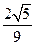
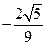
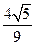
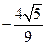
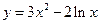 的单调增区间为
的单调增区间为 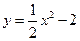 在点
在点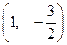 处切线的倾斜角为 ( )
处切线的倾斜角为 ( )