题目内容
如图，直角三角形PAQ的顶点P(－3,0)，点A在y轴上，点Q在x轴正半轴上，∠PAQ＝90°.在AQ的延长线上取点M，使
.
（1）当点A在y轴上移动时，求动点M的轨迹C；
（2）设轨迹C的准线为l，焦点为F，过F作直线m交轨迹C于G、H两点，过点G作平行轨迹C的对称轴的直线n且n∩l＝E.试问：点E、O、H（O为坐标原点）是否在同一条直线上？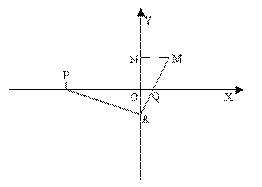
说理由.
解析： （1）设M(x,y)，且过点M作MN⊥OY于N 则
∴
∴点A坐标为
由题设得PA⊥AM 
化简得
① 注意到当x＝0时，点M与点N重合，点Q与原点重合，这与已知条件不符
因此，动点M的轨迹方程为 ， 其轨迹是顶点在原点，焦点为F(1,0)的抛物线（不含顶点）.
(2)由（1）知，轨迹C的焦点F(1,0)，准线l：x＝－1
（）当直线m不与x轴垂直时， 设直线m的方程为y＝k(x-1)（k≠0）①
将①与 联立，消去x得
∴由韦达定理得
②
又直线n的方程为
∴
∴
∴
∴点E、O、H三点共线
（）当直线m⊥ox时，直线m的方程为x＝1，此时易证点E、O、H三点共线.于是，由（）（）知，题设条件下的点E、O、H一定在同一条直线上.
∴
∴点A坐标为 由题设得PA⊥AM 化简得① 注意到当x＝0时，点M与点N重合，点Q与原点重合，这与已知条件不符因此，动点M的轨迹方程为
， 其轨迹是顶点在原点，焦点为F(1,0)的抛物线（不含顶点）.(2)由（1）知，轨迹C的焦点F(1,0)，准线l：x＝－1
（）当直线m不与x轴垂直时， 设直线m的方程为y＝k(x-1)（k≠0）①
将①与
联立，消去x得 ∴由韦达定理得 ②又直线n的方程为
∴ ∴ ∴
∴点E、O、H三点共线（）当直线m⊥ox时，直线m的方程为x＝1，此时易证点E、O、H三点共线.于是，由（）（）知，题设条件下的点E、O、H一定在同一条直线上.
练习册系列答案
相关题目
（2012•宝鸡模拟）如图，已知PA⊥平面ABC，且
（2012•宝鸡模拟）如图，已知PA⊥平面ABC，且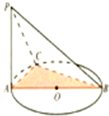
如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的任意一点，则图中直角三角形有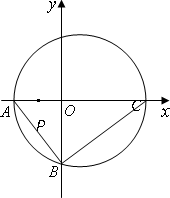
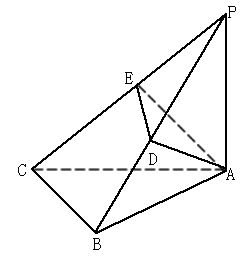
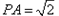)，顶点C在x轴上，点P为线段PA的中点．
，求该直线被圆M截得的弦长．
，等腰直角三角形ABC中，AB=BC=1，AB⊥BC，AD⊥PB于D，AE⊥PC于E。