题目内容
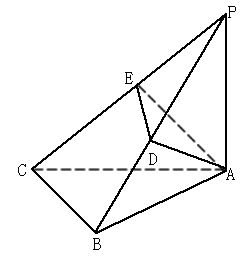
如图,已知PA⊥平面ABC,且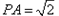 ,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E。
,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E。
(1)求证:PC⊥平面ADE;
(2)求点D到平面ABC的距离。
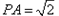 ,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E。
,等腰直角三角形ABC中,AB=BC=1,AB⊥BC,AD⊥PB于D,AE⊥PC于E。(1)求证:PC⊥平面ADE;
(2)求点D到平面ABC的距离。
解:(1)证明:因为PA⊥平面ABC,
所以 ,
,
又 ,且
,且 ,
,
所以BC⊥平面PAB,
从而 ,
,
又AD⊥PB, ,
,
所以AD⊥平面PBC,
得 ,
,
又 ,
,
所以PC⊥平面ADE。
(2)过D点作DF⊥BA,垂足为E,
由题意知DF⊥面ABC,即DF为所求距离,
由题设得DF∥PA,
所以△BDE ∽△BAP ,即DF= ,
,
又∵△BDA∽△BAP,
∴ 即BD=
即BD= ,
,
∴ ,
,
∴DE= ,
,
即点D到平面ABC的距离为 。
。
所以
 ,
,又
 ,且
,且 ,
,所以BC⊥平面PAB,
从而
 ,
,又AD⊥PB,
 ,
,所以AD⊥平面PBC,
得
 ,
,又
 ,
,所以PC⊥平面ADE。
(2)过D点作DF⊥BA,垂足为E,
由题意知DF⊥面ABC,即DF为所求距离,
由题设得DF∥PA,
所以△BDE ∽△BAP ,即DF=
 ,
,又∵△BDA∽△BAP,
∴
 即BD=
即BD= ,
,∴
 ,
,∴DE=
 ,
,即点D到平面ABC的距离为
 。
。
练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 (2012•丹东模拟)如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
(2012•丹东模拟)如图,已知PA⊥平面ABCD,ABCD是矩形,PA=AB=1, (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点. (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.