Question

    已知椭圆的中心在原点，长轴在x轴上，右顶点到右焦点的距离与它到右准线的距离之比为. 不过A点的动直线交椭圆于P,Q两点．

（1）       求椭圆的标准方程；

（2）证明两点的横坐标的平方和为定值；

（3）过点的动圆记为圆，已知动圆过定点和(异于点)，请求出定点的坐标.

Answer 1

解：（1）设椭圆的标准方程为.由题意得.……2分

, , ……2分   椭圆的标准方程为.……4分

（2）证明：设点

将带入椭圆，化简得：

,……6分  ,                          

P,Q两点的横坐标的平方和为定值4.……7分

（3）(法一)设圆的一般方程为:,则圆心为（）,

PQ中点M(),  PQ的垂直平分线的方程为:, ……8分

圆心（）满足，所以,……9分

圆过定点(2,0)，所以,……10分

圆过, 则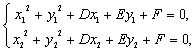 两式相加得：

 ,……11分

,    .……12分

因为动直线与椭圆C交与P,Q（均不与A点重合）所以，

由解得: ……13分

代入圆的方程为：,

整理得：,……14分

所以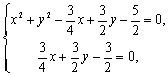：……15分   解得：或(舍).

     所以圆过定点(0,1).……16分

(法二) 设圆的一般方程为:,将代入的圆的方程:

.……8分

方程与方程为同解方程.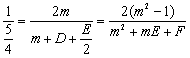, ……11分

圆过定点(2,0)，所以 ,  ……12分          

因为动直线与椭圆C交与P,Q（均不与A点重合）所以.

解得: ,……13分  (以下相同)