题目内容
20.设函数f(x)=x3+x,x∈R,若0<θ<$\frac{π}{2}$时,不等式f(msinθ)+f(1-m)>0恒成立.则实数m的取值范围是(-∞,1].分析 利用奇函数f(x)=x3+x单调递增的性质,可将不等式f(msinθ)+f(1-m)>0恒成立,转化为msinθ>m-1恒成立,由0<θ<$\frac{π}{2}$可求得实数m的取值范围.
解答 解:∵f(x)=x3+x,
∴f(-x)=(-x)3+(-x)=-x3-x=-f(x),
∴函数f(x)=x3+x为奇函数;
又f′(x)=3x2+1>0,
∴函数f(x)=x3+x为R上的单调递增函数.
∴f(msinθ)+f(1-m)>0恒成立?f(msinθ)>-f(1-m)=f(m-1)恒成立,
∴msinθ>m-1(0<θ<$\frac{π}{2}$)恒成立?m(1-sinθ)<1恒成立,
由0<θ<$\frac{π}{2}$知,0<sinθ<1,0<1-sinθ<1,$\frac{1}{1-sinθ}$>1
由m<$\frac{1}{1-sinθ}$恒成立知:m≤1.
∴实数m的取值范围是(-∞,1].
故答案为:(-∞,1].
点评 本题考查函数的奇偶性与单调性,突出考查转化思想与恒成立问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在梯形ABCD中,AB∥CD,且AB=2CD,设$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在梯形ABCD中,AB∥CD,且AB=2CD,设$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.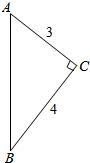 如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,求这个几何体的表面积与体积.
如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,求这个几何体的表面积与体积.