题目内容
【题目】已知圆柱![]() 底面半径为1,高为
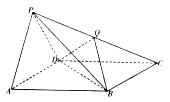
底面半径为1,高为![]() ,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线
,ABCD是圆柱的一个轴截面,动点M从点B出发沿着圆柱的侧面到达点D,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面ABCD绕着轴
如图所示.将轴截面ABCD绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点P.
相交于点P.
(Ⅰ)求曲线![]() 长度;
长度;
(Ⅱ)当![]() 时,求点
时,求点![]() 到平面APB的距离;
到平面APB的距离;
(Ⅲ)证明:不存在![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() .
.
【答案】(Ⅰ) ![]() (Ⅱ) 不存在
(Ⅱ) 不存在
【解析】试题分析:(Ⅰ)在侧面展开图中根据几何性质求解;(Ⅱ) 建立如图所示的空间直角坐标系,求出平面ABP的一个法向量及向量![]() ,利用空间向量点到直线距离公式求解;(Ⅲ)假设存在满足要求的
,利用空间向量点到直线距离公式求解;(Ⅲ)假设存在满足要求的![]() ,在空间坐标系中求出法向量,根据空间向量夹角余弦公式,列出关于
,在空间坐标系中求出法向量,根据空间向量夹角余弦公式,列出关于![]() 的方程,看是否有解即可.
的方程,看是否有解即可.
 试题解析:(Ⅰ)
试题解析:(Ⅰ) ![]() 在侧面展开图中为BD的长,其中AB = AD = π,
在侧面展开图中为BD的长,其中AB = AD = π,
∴![]() 的长为
的长为![]() ;
;
(Ⅱ)当![]() 时,建立如图所示的空间直角坐标系,
时,建立如图所示的空间直角坐标系,
则有![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() 、
、![]() 、
、![]()
设平面ABP的法向量为![]() ,则
,则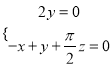 ,
,
取z = 2得![]() ,所以点C1到平面PAB的距离为
,所以点C1到平面PAB的距离为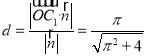 ;
;
注:本题也可以使用等积法求解.
(Ⅲ) 假设存在满足要求的![]() ,
,
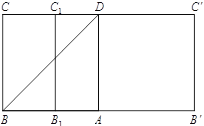 在(II)的坐标系中,
在(II)的坐标系中, ![]() ,
,
![]() ,
,
设平面ABP的法向量为![]() ,则
,则
![]() ,
,
取x1 = 1得![]() ,
,
又平面ABD的法向量为![]() ,
,
由二面角![]() 的大小为
的大小为![]() ,
,
则
![]() .
.
∵![]() ,∴
,∴![]() 时,均有
时,均有![]() ,与上式矛盾.
,与上式矛盾.
所以不存在![]() 使得二面角
使得二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目