题目内容
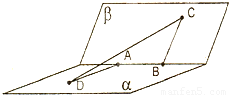
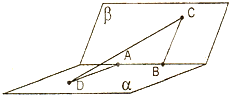
如图,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A、B到直线l(库底与水坝的交线)的距离AC和BD分别为a和b,CD的长为c,AB的长为d.求库底与水坝所成二面角的余弦值.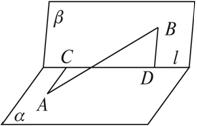
思路解析:所求二面角的平面角就是图中直线AC、BD所成的角.因此,利用向量的数量积求出这个角.
解:如题图,AC=a,BD=b,CD=c,AB=d.
根据向量的加法法则,![]() =
=![]() +
+![]() +
+![]() .
.
d2=![]() =(
=(![]() +
+![]() +
+![]() )2=a2+c2+b2+2
)2=a2+c2+b2+2![]() ·
·![]()
=a2+c2+b2-2![]() ·
·![]() .
.
于是,得2![]() ·
·![]() =a2+c2+b2-d2.
=a2+c2+b2-d2.
设向量![]() 与
与![]() 的夹角为θ,θ就是库底与水坝所成的二面角.
的夹角为θ,θ就是库底与水坝所成的二面角.
因此2abcosθ=a2+c2+b2-d2,
所以cosθ=![]()
即库底与水坝所成的二面角的余弦值为![]()
方法归纳 立体几何中的夹角,都可以转化为两个向量的夹角.向量u和v的夹角θ满足关系式cosθ=![]() .立体几何中有关夹角问题,经常用空间向量的数量积解决.
.立体几何中有关夹角问题,经常用空间向量的数量积解决.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,已知测得从D、C到库底与水坝的交线的距离分别为
如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,已知测得从D、C到库底与水坝的交线的距离分别为 处,乙站在水坝斜面上的点
处,乙站在水坝斜面上的点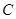 处,已知测得从
处,已知测得从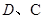 到库底与水坝的交线的距离分别为
到库底与水坝的交线的距离分别为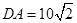 米、
米、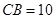 米,
米,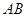 的长为
的长为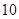 米,
米,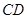 的长为
的长为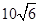 米,则库底与水坝所成的二面角的大小 度.
米,则库底与水坝所成的二面角的大小 度.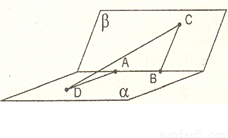
 处,乙站在水坝斜面上的点
处,乙站在水坝斜面上的点 处,已知库底与水坝所成的二面角为
处,已知库底与水坝所成的二面角为 ,测得从
,测得从 到库底与水坝的交线的距离分别为
到库底与水坝的交线的距离分别为 米、
米、 米,又已知
米,又已知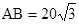 米,则甲乙两人相距( )米.
米,则甲乙两人相距( )米. 
 C.
60 D. 70
C.
60 D. 70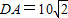 米、CB=10米,AB的长为10米,CD的长为
米、CB=10米,AB的长为10米,CD的长为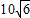 米,则库底与水坝所成的二面角的大小为 度.
米,则库底与水坝所成的二面角的大小为 度.