题目内容
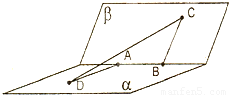
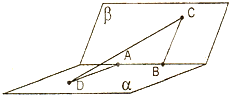 如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,已知测得从D、C到库底与水坝的交线的距离分别为DA=10
如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,已知测得从D、C到库底与水坝的交线的距离分别为DA=10| 2 |
| 6 |
135
135
度.分析:利用向量的运算法则和模的计算公式、二面角的定义即可得出.
解答:解:如图所示,
=
+
+
,
∴
2=(
+
+
)2=
2+
2+
2+2
•
+2
•
+2
•
,
∵
⊥
,
⊥
,∴
•
=
•
=0.
又|
|=10
,|
|=10,|
|=10,|
|=10
.
∴(10
)2=(10
)2+102+102+2×10
×10cos<
,
>,
解得cos<
,
>=
,∴<
,
>=45°.
∴库底与水坝所成的二面角=180°-45°=135°.
故答案为135°.
| DC |
| DA |
| AB |
| BC |
∴
| DC |
| DA |
| AB |
| BC |
| DA |
| AB |
| BC |
| DA |
| AB |
| DA |
| BC |
| AB |
| BC |
∵
| DA |
| AB |
| AB |
| BC |
| DA |
| AB |
| AB |
| BC |
又|
| DA |
| 2 |
| BC |
| AB |
| DC |
| 6 |
∴(10
| 6 |
| 2 |
| 2 |
| DA |
| BC |
解得cos<
| DA |
| BC |
| ||
| 2 |
| DA |
| BC |
∴库底与水坝所成的二面角=180°-45°=135°.
故答案为135°.
点评:熟练掌握向量的运算法则和模的计算公式、二面角的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
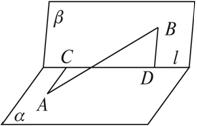
 处,乙站在水坝斜面上的点
处,乙站在水坝斜面上的点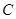 处,已知测得从
处,已知测得从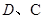 到库底与水坝的交线的距离分别为
到库底与水坝的交线的距离分别为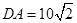 米、
米、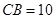 米,
米,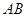 的长为
的长为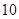 米,
米,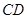 的长为
的长为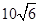 米,则库底与水坝所成的二面角的大小 度.
米,则库底与水坝所成的二面角的大小 度.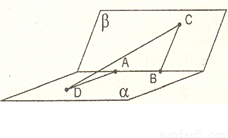
 处,乙站在水坝斜面上的点
处,乙站在水坝斜面上的点 处,已知库底与水坝所成的二面角为
处,已知库底与水坝所成的二面角为 ,测得从
,测得从 到库底与水坝的交线的距离分别为
到库底与水坝的交线的距离分别为 米、
米、 米,又已知
米,又已知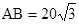 米,则甲乙两人相距( )米.
米,则甲乙两人相距( )米. 
 C.
60 D. 70
C.
60 D. 70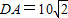 米、CB=10米,AB的长为10米,CD的长为
米、CB=10米,AB的长为10米,CD的长为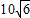 米,则库底与水坝所成的二面角的大小为 度.
米,则库底与水坝所成的二面角的大小为 度.