题目内容
如图2-5-16，P为圆O外一点，PA、PB是圆O的两条切线，A、B为切点，OP与AB相交于点M，且点C是AB上一点.求证：∠OPC=∠OCM.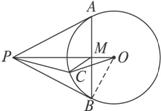
图2-5-16
思路分析:图形中有两条切线，故运用切割线定理得线段和角的关系，在Rt△OPB中运用射影定理，有OB2=OP·OM，代换其中的OB为OC，可得三角形相似，即得角的相等关系.
证明:连结OB，由切线长定理，得PA=PB,PM⊥AB，PO平分∠APB.
又PB⊥OB，在Rt△OPB中，OB2=OP·OM，∵OB=OC，∴OC2=OP·OM,即
.
∴△OCP∽△OMC.∴∠OPC=∠OCM.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
如图，设圆（x-5）2+y2=16的圆心为C，此圆和抛物线y2=px（p＞0）有四个交点，若在x轴上方的两个交点为A（x1，
（2012•江苏）A．[选修4-1：几何证明选讲]
的图象按向量y=(-1,0)平移，得到的图象对应的函数表达式为y=
相交，所得弦长为2
+
)=
，sin(
,则tan