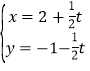题目内容
【题目】已知圆![]() :
:![]() ,过
,过![]() 且与圆
且与圆![]() 相切的动圆圆心为
相切的动圆圆心为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,垂足为
,垂足为![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() 为不同的四个点).
为不同的四个点).
①设![]() ,证明:
,证明:![]() ;
;
②求四边形![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() .(2)①见解析.②
.(2)①见解析.②![]() .
.
【解析】试题分析:
(1)设动圆半径为![]() ,由于
,由于![]() 在圆内,圆
在圆内,圆![]() 与圆
与圆![]() 内切,由题意可得
内切,由题意可得![]()
![]() ,则点
,则点![]() 的轨迹
的轨迹![]() 是椭圆,其方程为
是椭圆,其方程为![]() .
.
(2)①由题意可知![]() ,而
,而![]() ,
,![]() ,
,![]() ,
,![]() 为不同的四个点,故
为不同的四个点,故![]() .
.
②若![]() 或
或![]() 的斜率不存在,四边形
的斜率不存在,四边形![]() 的面积为
的面积为![]() .否则,设
.否则,设![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程可得
,联立直线方程与椭圆方程可得![]() ,同理得
,同理得![]() ,则
,则![]()
![]()
![]()
![]() ,当且仅当
,当且仅当![]() 时等号成立.则四边形
时等号成立.则四边形![]() 的面积取得最小值为
的面积取得最小值为![]() .
.
试题解析:
(1)设动圆半径为![]() ,由于
,由于![]() 在圆内,圆
在圆内,圆![]() 与圆
与圆![]() 内切,
内切,
则![]() ,
,![]() ,
, ![]()
![]() ,
,
由椭圆定义可知,点![]() 的轨迹
的轨迹![]() 是椭圆,
是椭圆,![]() ,
,![]() ,
,![]() ,
,
![]() 的方程为
的方程为![]() .
.
(2)①证明:由已知条件可知,垂足![]() 在以
在以![]() 为直径的圆周上,
为直径的圆周上,
则有![]() ,
,
又因![]() ,
,![]() ,
,![]() ,
,![]() 为不同的四个点,
为不同的四个点,![]() .
.
②解:若![]() 或
或![]() 的斜率不存在,四边形
的斜率不存在,四边形![]() 的面积为
的面积为![]() .
.
若两条直线的斜率存在,设![]() 的斜率为
的斜率为![]() ,
,
则![]() 的方程为
的方程为![]() ,
,
解方程组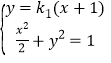 ,得
,得![]()
![]() ,
,
则![]() ,
,
同理得![]() ,
,
∴![]()
![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
综上所述,当![]() 时,四边形
时,四边形![]() 的面积取得最小值为
的面积取得最小值为![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目